Table of Contents
Chapter: Stretch, fold, prune
(ChaosBook.org blog, chapter Qualitative dynamics, for cyclists) — Predrag Cvitanovic 2009-02-11 12:55
Section: Going global: stable/unstable manifolds
Predrag 2009-03-05 added new text on construction of unstable manifolds, arclength parametrization, return maps - still in progress
Section: Prune danish
I don't care for islands, especially very small ones.
D.H. Lawrence
Predrag Oct 29 2009 to Jorge Kurchan: Here are three simple exercises for clones to go fishing:
- ChaosBook.org exercise 3.6. How strange is the Hénon attractor? (if clones are smart, they should return a least unstable periodic orbit of length 13 whose symbol sequence which is - I hope - mentioned later in ChaosBook)
- For many years it was believed that 2-dimensional (xy)2 potential is chaotic. This was killed by P. Dahlqvist and G. Russberg, “Existence of stable orbits in the x2y2 potential”, Phys. Rev. Lett. 65, 2837 (1990). Exercise: let clones find the shortest period elliptic island.
- Gutzwiller still believes that for sufficiently large anisotropy anisotropic Kepler problem is chaotic, and has done extensive numerics to check that. I (and, for example, Devaney) believe that the islands are most likely so small that one cannot find them without detailed topological intuition of where they would pop up (that's what was needed to kill the conjecture 1). Exercise: Let clones find any elliptic island for Gutzwiller value of anisotropy.
1. and 2. were done by thinking, I'll be impressed if the clones nail them. You would do community a service if you kill “the ergodicity” of anisotropic Kepler problem.
Finally, make sure you do not cite this paper (nobody with taste ever cites these guys):
I'm on your wavelength in P. Cvitanović, A. Artuso and B. Kenny, "Phase transitions on strange irrational sets" Phys. Rev. A 39, 268 (1989): τ in that paper is your Darwinian parameter, it picks out the most stable/unstable orbit in ±∞ limit. This paper was on the way to learning how to cycle, no cycle expansions yet, but it was the first one to introduce phase transitions in the context of deterministic non-wandering sets, so focus is not on the extreme events, but on the phase transition values, where things can go either way, and all orbits contribute. Recycling was done in R. Artuso, E. Aurell and P. Cvitanović "Recycling of strange sets: II. applications" , where Fig 12 shows the extremal periodic orbit.
Jorge Oct 29 2009 I take it when you say 'chaotic' you mean purely chaotic, with no islands whatsoever, right?
Predrag Oct 29 2009 Yep! Chaotic = rigorously ergodic, ie, every open set within the nonwandering set can be reached, ie, no attractive sub-basins, or elliptic regions (for Hamiltonian flows).
Jorge and Khan Dang Nov 18 2009 We have looked at the x2y2 potential with our program. The program finds the known island in ten minutes or so, but forbidding this one, have also found another much smaller one.
Khan Dang Nov 18 2009 j'ai trouvé un tout petit ilôt de taille 2e-5 × 5e-5. J'ai mis un piège mortel sur l'ilôt de stabilité déjà découvert en 1990 (cet ilôt était beaucoup beaucoup plus gros, environ 1e-3 × 5e-4 !). Ci-joint:
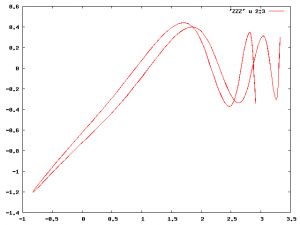
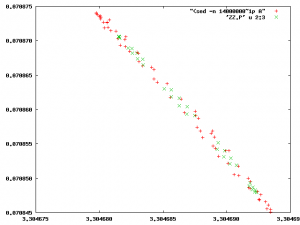
(left) La trajectoire stable au centre de l'ilôt dans l'espace réel.
(right) Quelques clones en rouge ; en vert, une ellipse de stabilité calculée en intégrant directement les équation du mouvement.
Predrag Nov 21 2009 Congratulations! Please also identify the symbolic dynamics of the new island.
Nobody every listens to me, but if you guys decide to split from the common and violate the rule, read ChaosBook.org chapter World in a mirror. In x2y2 you want to work in the fundamental domain of D4 symmetry group, and for the anisotropic Kepler the symmetry is D1. It will save you many clones, especially if you restrict cloning to invariant subspaces, I believe.
As to details: teach your graphics routine to use the same units in the x and y axis - nicer to see the symmetry than to see it squashed. Square is a square.
Jorge Oct 29 2009 Julien Tailleur and Khanh-Dang Nguyen Thu Lam are now attacking the anisotropic Kepler. Question: do you expect the system to have large regular islands when the anisotropy is very large? Is there a 'maximal chaos' anisotropy value, for which you expect the system to be at its most chaotic?
Predrag Nov 21 2009 The system is integrable in isotropic limit and presumably also in the extreme anisotropic limit. Don't know where the 'maximal chaos' anisotropy value lies. I would start fishing at the Broucke island anisotropy (refered to in F. Christiansen and P. Cvitanović "Periodic orbit quantization of the anisotropic Kepler problem", CHAOS 2, 61 (1992)) and keep increasing anisotropy, see how far on can go and clones still work. Good luck fishing.
And don't knock the exercise 3.6; if you can kill the ergodicity of the Hénon attractor without thinking, Fields Medal cannot be far behind.
Julien Tailleur Nov 21 2009 I think the entries in the blog should not have more than 140 characters, otherwise it smells too much of XXth century.
Cloning 'on the attractor' for the Hénon map: One thing we saw during my Ph.D. is that if you don't restrict your noise to be tangent to the attractor, you can stabilize stuff outside. For instance in the dissipative standard map, we stabilized the original separatrix. If we want to do something for dissipative cases, we have to think a bit about that. A cheap way would be to start the code without noise, wait for the dynamics to converge to the attractor and start the noise afterwards (and pray that the clones don't diffuse outside) but that's not really nice and probably won't work. Another way would be to apply the noise only when the cloning happens. I think in this case I remember a paper by Ott who says that the convergence 'back' to the attractor is pretty fast.
Also we could use the cloning the way Grassberger does: wait till one clone's weight is 1.5 and clone with p=0.5 (and put back the weight(s) to 1) or if the weight first reaches 0.5, kill with probability 1/2 or put the probability back to 1 with probability 1/2. This way we would apply the noise less often and may stick better to the attractor.
Predrag Nov 24 2009 Reread F. Christiansen and P. Cvitanović "Periodic orbit quantization of the anisotropic Kepler problem", CHAOS 2, 61 (1992). Cute what one can write when one is the editor of a special issue of CHAOS and not plagued by referees. Not at all a nice hyperbolic system, and -baring a new idea of how to take care of the y-axis collision orbit analytically- still not well understood. Amusing read, but will not be helpful to cloning. Freddy computed about 20,000 cycles (cycle lengths are a bit complicated - explained on p. 65), and they are all hyperbolic, arranged in sensibly converging families, with no hint of non-hyperbolicity anywhere to help guide the clones. Still think best to start with Broucke island anisotropy, keep increasing it, see for how long the clones can find islands.
Predrag Dec 12 2009 to Divakar maybe related to your Complex singularities and the Lorenz attractor:
Does the complex susceptibility of the Henon map have a pole in the upper-half plane ?
Actually, replacing pruned parabola periodic orbits by complex periodic orbits (Julia set) would already be nice
Predrag Feb 8 2010 to Parisians Extreme fluctuations and the finite lifetime of the turbulent state by Nigel Goldenfeld, Nicholas Guttenberg and Gustavo Gioia might be of interest to you. I have no good idea how to set up clones to do this. You could use Channelflow to integrate in a small plane Couette cell reasonably fast (pipe simulations are probably much slower). Keeping track of Lyapunov eigen-exponents is much more costly; Gibson and Viswanath do it by Arnoldi-Krylov methods, for equilibria and periodic orbits. As far as I know, no one yet has implemented it as a covariant Lyapunov vectors calculation. Decay to laminar state is marked by lots of almost marginal eigenvalues; that's presumably the “extreme event” signature.
Predrag Mar 11 2010 Multicanonical sampling of rare trajectories in chaotic dynamical systems by Akimasa Kitajima and Yukito Iba: “Multicanonical Monte Carlo” can estimate the probability of initial conditions that lead to trajectories of a given level of chaoticity. They cite references [7, 8, 9, 10, 11] “that discuss sampling of unstable periodic orbits in chaotic systems by dynamic Monte Carlo or related methods”. Should have a look at these…
- [7] Sasa, S.-i. and Hayashi, K., EPL (Europhysics Letters) 74 (2006) 156.
- [8] Kawasaki, M. and Sasa, S.-i., Phys. Rev. E 72 (2005) 037202.
- [9] Takeuchi, K. and Sano, M., Phys. Rev. E 75 (2007) 036201.
- [10] Pratt, L. R., J. Chem. Phys. 85 (1986) 5045.
- [11] Cho, A., Doll, J., and Freeman, D., Chemical Physics Letters 229 (1994) 218
I emailed them the 3 problems above, asked them to test their method on them.
Predrag Mar 12 2010 Akimasa Kitajima reponded: “I will inform you when we get results on them.”
John Mar 12 2010 Good find, seems entirely relevant, will review.
Predrag Mar 13 2010 If you do read any of them, please do me a favor and blog your notes as you read them, either here (this is public) or siminos/blog (that is internal). Helps all of us in figuring what literature to read/not to read.
Predrag Apr 21 2010 Identifying rare chaotic and regular trajectories in dynamical systems with Lyapunov weighted path sampling by Philipp Geiger and Christoph Dellago is the next interesting paper in this series, with applications to yet another set of examples. I emailed them the 3 problems above, asked them to test their method on them.
Predrag May 6 2011 The monodromy theory of complex dynamical systems approach to the pruning front, http://www.cris.hokudai.ac.jp/arai/papers/loops.pdfOn loops in the hyperbolic locus of the complex Henon map and their monodromies by the mathematician and drummer Zin Arai of the Creative Research Institute looks very interesting (but what makes “Non Traditional Science” non-traditional? Go figure).
~~DISCUSSION~~
