Table of Contents
Chapter: Noise
(ChaosBook.org blog)
to find recent edits: click on [Recent changes], select changed page, then [Old revision], compare versions
Noise blog
enter the latest posts at the top of this section
2010-08-03 PC to Domenico Noise reduces disorder in chaotic dynamics by Denis S. Goldobin and Michael A. Zaks. They say: “We evoke the idea of representation of the chaotic attractor by the set of unstable periodic orbits and discover a novel noise-induced ordering phenomenon. For long unstable periodic orbits the weights (or natural measure) appear to be highly inhomogeneous over the set either diminishing or enhancing their contribution into system dynamics. We show analytically a weak noise to reduce this inhomogeneity and, additionally to obvious perturbing effect, make a regularizing influence on the chaotic dynamics. We demonstrate this universal effect rooted into the nature of deterministic chaos for the Lorenz system. The effect can be observed as shrinking of the distribution of averages over finite segments of the chaotic trajectory and lead to significant enhancement of the coherence of chaotic oscillations.”
2010-07-02 PC to Sara They probably exist - Google returns lots of hits of type “Rayleigh–Rice distribution”…“Lagruerre polynomials” etc. Check it out. There exist also orthogonal Rice polynomials (hypergeometric functions) but I think they are not related to the Rice distribution.
2010-07-01 Sara What would be really useful is a family of orthogonal PDFs. If you coma across such thing …
2010-07-01 PC to Sara Rice distribution (see wikipedia and MathWorld noise might be the right distribution to use in your work on linear-nonlinear models. I was told that it describes the distribution of distances between two random events. There is also a Rayleigh Distribution. The original paper is Stephen O. Rice, “Statistical properties of a sine wave plus random noise,” Bell Syst. Tech. J. 22 109–57 (1948 ). [7] Nakagami M 1960 The m-distribution—a general formula
2010-04-07 PC In Goettingen Mirko … and David Hofmann have started an interesting Stochastic Processes Seminar.
2009-12-08 PC to Domenico State and parameter estimation using Monte Carlo evaluation of path integrals by John C. Quinn and Henry D.I. Abarbanel might be of interest for your thesis preparation. They say: “ Transferring information from observations of a dynamical system to estimate the fixed parameters and unobserved states of a system model can be formulated as the evaluation of a discrete time path integral in model state space. The observations serve as a guiding potential working with the dynamical rules of the model to direct system orbits in state space. The path integral representation permits direct numerical evaluation of the conditional mean path through the state space as well as conditional moments about this mean. ”
They use (if not in this paper, than in the earlier ones ) the same convolution of noise variance and trajectory variance as we, as a part of the Kalman filter procedure. I think I reported on some of that in my notes on the Paris Lyapunov vectors conference, svn siminos/blog, and there is a mention of Kalman filters in stoch/flotsam.tex. We also heard Ott talk about use of Kalman filters by the Maryland group weather prediction work.
As far as is plumbing is concerned, I think we might need something like that to marry our statespace picture of turbulent flows (computed in the full 3-dimensional Navier-Stokes) with partial information obtained in experiments (typically a full 3-dimensional velocity field, fully resolved in time, but measured only on a 2-dimensional disk section across the pipe). The challenge is to match this measurement of the turbulent flow with a statespace point in our 100K ODE representation, and then track the experimental observation to improve our theoretical prediction for the trajectory in the time ahead. That would be the absolutely best “weather prediction” attainable for a turbulent pipe flow, limited by a combination of Lyapunov time and observational noise. In our parlance, the “optimal partition of statespace”.
2009-10-23 PC to Domenico Random fluctuation leads to forbidden escape of particles by C. S. Rodrigues, A. P. S. de Moura, and C. Grebogi might be of interest to you. They say: “We show that, under finitely small random fluctuations of the field, trajectories starting inside KAM islands escape within finite time. The non-hyperbolic dynamics gains then hyperbolic characteristics due to the effect of the random perturbed field. As a consequence, trajectories which are started inside KAM curves escape with hyperbolic-like time decay distribution. We show a universal quadratic power law relating the exponential decay to the amplitude of noise.”
How well can one resolve the state space of a chaotic flow?
the latest pdf version of DasArtikel
(append posts at the end of a section, in sections named after people)
 Accepted for publication in Phys Rev Letters — Predrag Cvitanovic 2009-12-16 00:10
Accepted for publication in Phys Rev Letters — Predrag Cvitanovic 2009-12-16 00:10
 now on
now on arXiv:0902.4269 and submitted to Phys Rev Letters — Predrag Cvitanovic 2009-03-08 17:18
 If you have time and inclination, have a look at
ChaosBook.org/~predrag/papers/pubs.html. It is our latest crack on the
noise problem, differs quite a bit from papers 1-3. Word `quantum'
is not mentioned, but something like that should also
perhaps replace Berry-Keating cycle expansion cutoff, and Hermite
basis should be also a natural basis for semi-classical corrections
calculations.
Grateful for any criticisms, references etc.
— Domenico & Predrag 2009-01-14
If you have time and inclination, have a look at
ChaosBook.org/~predrag/papers/pubs.html. It is our latest crack on the
noise problem, differs quite a bit from papers 1-3. Word `quantum'
is not mentioned, but something like that should also
perhaps replace Berry-Keating cycle expansion cutoff, and Hermite
basis should be also a natural basis for semi-classical corrections
calculations.
Grateful for any criticisms, references etc.
— Domenico & Predrag 2009-01-14
Domenico & Predrag
 it would be good to check a few things before the referee reports arrive:
it would be good to check a few things before the referee reports arrive:
- Continuing on discussion with Carl, text from me to you next to numerical estimates of escape rates: “make sure that the noiseless Fredholm determinant is converging super-exponentially, as it should, and that the noisy cycle expansions are not converging to the noiseless answer, as this graph seems to indicate:” — Predrag Cvitanovic 2009-03-10 09:16
- Further down you say: “The fact that adding 0110 and 0111 does not change the determinant at all is probably an accident. In the case of the quartic map, the determinant of the optimal partition differs greatly from the one given by the partition immediately simpler, but their leading zeroes only differ by 10^{-5}”
- Can you enter your transition graph, determinant into stoch.tex, isolate the terms that differ from the partition we are currently using, look at their values and geometrical (state space) placement carefully so we understand why they “shadow”? — Predrag Cvitanovic 2009-03-10
- I have rewritten ChaosBook chapters "Walkabout: Transition graphs" and "Counting" to include the discussion needed for your thesis, you might have a look at them, see whether they are more helpful now — Predrag Cvitanovic 2009-02-20
Marcos Saraceno
![]() My "noisy" papers are always related to 2D quantum systems and although related, are pretty far from your case. On the other hand..
My "noisy" papers are always related to 2D quantum systems and although related, are pretty far from your case. On the other hand..
- For a long time my group, especially Eduardo Vergini, has been pushing the idea of 'short periodic orbit quantization', which consists essentially in putting deformed gaussian wave packets with the proper classical phases on selected short (with respect to the Heisenberg time) periodic orbits and using that as a basis in which to look at the dynamics. (You can look at L. Ermann and M. Saraceno, A periodic orbit basis for the Quantum Baker Map, Phys. Rev. E 78, 036221 (2008), for a nice application to the baker's map). It seems to me that you are doing something similar, albeit with the VERY BIG difference of a 1D dissipative and classical map.
- what was very interesting for me about your paper is that the map you are using (with a little rectification of the two branches f_0,f_1) can be easily made 2D and quantized to an open 2D map (of the baker type) (see i.e. Saraceno, Vallejos, Chaos 6 , 193,1996). This is a kind of open map with a lot of current interest (see recent papers by Nonnenmacher, Keating, Wisniacki). I wonder if a basis of deformed gaussian packets would fare as well in the quantum case. We are currently working on various open bakers, and this can be a very attractive idea.
- Next year? (check www.tandar.cnea.gov.ar/grupos/QCG)
— Marcos Saraceno 2009-01-28
- Predrag to Marcos: I have Eduardo Vergini on Domenico and my reading list, but we are way behind. In 2D Domenico has focused on the Lozi map, but you might be right - your baker maps are easier, he might check the optimal noise partitioning for the hyperbolic case on your models first.
— Predrag Cvitanovic 2009-01-28 07:44
Carl P.Dettmann
![]() I fear the editors of PRL will deem that the average experimental semiconductor or optical physicist will not be able to make sense of this. If so, you could always try Nonlinearity…
I fear the editors of PRL will deem that the average experimental semiconductor or optical physicist will not be able to make sense of this. If so, you could always try Nonlinearity…
- Predrag to Carl: No reason why an experimentalist should use this - that is not required. We tried mightily to dumb it down, but there are several ideas in it:
- noise limits partition refinements
- linearized adjoint Fokker-Planck tells you how
- Fokker-Planck is now a finite matrix
- each cycle point has a well defined width given by the leading Hermite eigenfunction
- Spectrum is given by determinant of the transition graph
The paper wants to get the concept of optimal partition, rest is mechanics and cross-checking. Do you see what we could remove? (rest of your comments as to what to add) Carl to Predrag: Just my interpretation of PRL criteria, which is about relating it to applications as well as dumbing down (particularly the intro). I don't see what can easily be removed.
- I think the general approach is right, modulo discontinuities as the diffusion constant is varied. This is reminiscent of stability ordering (Dettmann + Morriss, PRL 78, 4201 (1997)), for which smoothing helps (Dettmann + Dahlqvist, PRE 57, 5303 (1998)).
- Predrag to Carl: Not sure how this will pan out - remember, deterministic D is a fractal function of map parameters, this too might be getting more fractal as function of decreasing D. Dunno.
- Carl to Predrag: My intuition so far suggests gamma is a smooth function of D, despite increasing complexity of cycles.
- I am a bit concerned that the partition containing all periodic orbits is said to converge to the wrong answer. There is good numerical evidence that it works in general. I think it is more likely that it has not converged at this point; more data would help to clarify this.
- Domenico to Carl : The partition containing all periodic orbits converges to a different answer, that is the leading eigenvalue of the noisy evolution operator, which corresponds to the escape rate of the repeller from the support of the operator, which is larger than the unit interval. What I mean to find here is the escape rate from the unit interval, which I think is more meaningful (whatever maps out of the unit interval hardly comes back into it). I also did my blind-grid calculation only using the unit interval, unlike in the paper on local matrix approximation . I also tried the whole same procedure (find optimal partition, calculate escape rate, do the same including all orbits, compare w/ grid method) for the quartic repeller defined in your previous papers, and I got the same results as for the cubic map.
- Carl to Domenico : Thanks for this, which was not apparent from my (probably too quick) reading of the paper. Clearly restricting to the unit interval reduces the trace of noisy periodic orbits close to the boundary. I happen to think the “natural” escape rate is the limiting one for a very large interval, which in practice does not have to be larger than the unit interval extended by a few times the size of the noise. However, for the restricted version, the interval must be explicitly taken into account; for your new method this seems easily accomplished by using the domain of integration, but it should be possible also for the analytical expressions for the traces in terms of periodic orbits in powers of the noise strength.
* Predrag to Domenico : I am very concerned - at some point we need to make sure that the noiseless Fredholm determinant is converging superexponentially, as it should, and that the noisy cycle expansions are not converging to the noiseless answer, as this graph seems to indicate:
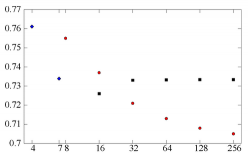 The escape rate
The escape rate  of the repeller
plotted as function of number of partition intervals
of the repeller
plotted as function of number of partition intervals  ,
estimated using:
(
,
estimated using:
( ) under-resolved 4-interval and
the 7-interval `optimal partition',
(
) under-resolved 4-interval and
the 7-interval `optimal partition',
( ) all periodic orbits of periods
up to
) all periodic orbits of periods
up to  in the deterministic, binary symbolic dynamics,
with
in the deterministic, binary symbolic dynamics,
with  periodic-point intervals (the deterministic,
noiseless escape rate is
periodic-point intervals (the deterministic,
noiseless escape rate is  ), and
(
), and
( ) a uniform discretization
in
) a uniform discretization
in  intervals. For
intervals. For  discretization yields
discretization yields  .
.
~~CL~~
- Predrag to Carl: You put your finger on it - we claim that not using the noise limited optional partition gives you a wrong answer. If Domenico's calculations are right, including more cycles takes you monotonically away from the correct answer, does not look like that this sequence in Table 1 is coming back. If you check with the quantum mechanics in your hallway, they will probably agree: going beyond Berry-Keating cycle expansion cutoff and not using unitarity for the rest is probably getting you a wrong answer. But this indeed is a bold claim, and Domenico and I are not sure about it, that is why it is not spelled out in the paper. And it is certainly not the point of the paper, this is a letter about the optimal partition, not about perturbation theory, so we have framed our numerical tests in a cautions way. What is interesting is that the 7-node transition matrix seems to give a darn good estimate.
- Carl to Predrag: OK - numerical evidence is that the coefficients of powers of D converge nicely with cycle length. Their sum is of course an asymptotic series, so the best easy approach is to truncate at the smallest term, then worry about how to resum the divergent tail. Your partition is likely a more sophisticated way of stopping at this point. Either way, there is no EXACT result using cycles (so far), just an approximation.
- The numerical data is too sparse to be convincing. Why not a plot of gamma against D, showing the discontinuities of this as D is varied, cf the exact value, and the original methods. Otherwise it just looks as if you picked a D that just happened to give the correct value.
- Predrag to Carl: Domenico has done tons of calculations which are documented in notes for the long paper and/or thesis on his subversion repository. That is for a long paper. But this is a Phys Rev Letter, and we only want to state the optimal partitioning hypothesis, and use one numerical test as an illustration.
- Carl to Predrag: I am suggesting only a single figure, which can probably replace the table. It shouldn't add much if any length, but will substantially add to the results.
Carl to Predrag (Jan 29, 2009, after addition of the above figure): The figure is clear, although not quite what I was asking for (gamma vs D). I can now think of another reason the “conventional” noisy periodic orbit theory doesn't appear to give the same answer - because Domenico is calculating the escape rate from the unit interval, the contribution from the periodic orbit on the edge of the domain should be half of what it would be on a more extended domain. A single incorrect periodic orbit weight doesn't lead to the wrong answer, but sure slows convergence.
— Carl P.Dettmann 2009-01-14 07:40
- Domenico to Predrag: The fact that adding 0110 and 0111 does not change the determinant at all is probably an accident. In the case of the quartic map, the determinant of the optimal partition differs greatly from the one given by the partition immediately simpler, but their leading zeroes only differ by 10^{-5}. This is the “shadowing” I once mentioned, and it may be good news, since that way the method seems stable, no matter whether we take one or two std. deviations as our overlapping criterion we get pretty much the same result. When I say “actually you shouldn't add any more cycles”, I mean that if you resolve further beyond the optimal partition (as it happens in our example if you split 00 into 000 and 001 and so on), you don't get the same result, but the escape rate drifts away from the value computed w/ the grid method.
- Domenico to Predrag : your paper “Spectrum of stochastic evolution operators: Local matrix representation approach” (with C.P. Dettmann, G. Palla, N. Søndergård and G. Vattay), Phys. Rev. E 60, (1999), says on page 3939 that the trace of the evolution operator on a periodic orbit p (our t_p) is ultimately equal to 1/|1-Λ_p| in the noiseless case.
Gregor Tanner
It seems you are constructing a basis localised on periodic orbits using the fact that the eigenfunction of the linearised flow are also approximate eigenfunctions of the full flow. — Gregor Tanner 2009-02-01 14:59
- I am struggling a bit to understand the cut-off criterion. When you look at this overlap criterion, are you taking periodic orbits of different length or do you use periodic orbits of the same length. (In the figure 8 there are 8 peaks, but somehow you count 000 and 001 as one orbit.) If you are somehow going for a basis supported by a neighborhood of period 3 orbits, why do you not chose the (simpler) transition graph based on the 8 period 3 orbits - that is, how significant is the 7 versus 8 change.
- Domenico : The overlapping criterion applies in principle to periodic points of orbits of different length as well as of the same. In the example shown, it turns out that the escape rate differs by about 0.1% from the one we reported, if 00 is split into 000 and 001.
- Obviously, your criterion will only recover the leading eigenvalue of L; if for some odd reason you want to calculate higher order eigenvalues - how would you need to change your basis in order to capture this? Can one give a general criterion (some sort of Heisenberg time) which tells you how many orbits you need to get a certain parts of the spectrum. And would a similar overlap criterion apply using longer orbits?
- Domenico : I don't see why, in principle, one cannot compute other eigenvalues: a finite partition results in a finite transition matrix, which in general has more than one eigenvalue. The determinant of the graph, which is now a polynomial, does have more than one root. The number of eigenvalues is now finite, but perhaps that's part of our claim: that information was wiped out by noise. In practice, I haven't computed any of those higher eigenvalues, so I can't say whether our method works or not to that extent.
- Predrag : I do not know how the non-leading eigenvalues will work out. The problem here is that we do not know what they are good for when computing escape rate - the first one gives rate of convergence to the natural repeller measure? Wirzba computed tons of the classical Perron-Frobeniou-Ruelle-Araki-… for the 3-disk problem (where at least we know that the quantum ones have to do with resonances), so if needed, we could try. — Predrag Cvitanovic 2009-02-04 02:29
- On a more technical note, how many eigenfunctions do you need in order to calculate a given trace; that is, in eqn (12), how big is the matrix for a given a→b? Also, shouldn't it be
 in eq (5) (otherwise (2) and (5) are identical.)
in eq (5) (otherwise (2) and (5) are identical.)- Domenico : For the two fixed points I used 32×32 matrices, for the rest of the periodic orbits I used 16×16. Equations (2) and (5) differ by the variable of integration (dx in (2) and dy in (5)). You can easily check that the two operators are adjoint to each other.
- Is there a minus sign missing in Eq (6) - or do I misunderstand the equation?
- Domenico : The left-hand side of the equation is the width of the Gaussian n steps of iteration before the point x_a, so the right-hand side should (and is) greater, if that's what you meant.
Gábor Vattay
It seems I should read DasArtikel — Vattay Gábor 2009-01-28
Daniel Braun
I have been extremely busy, preparing for a leave to the US tomorrow (I will spend half a year at the JQI, University of Maryland). I can have a look at your paper next week (>= Wednesday)
— Daniel Braun 2009-02-04 02:38
