Table of Contents
Continuation
2009-2-13
Continuation is finding a solution to an equation by using a solution to a nearby equation as an initial guess.
E.g. poor man's continuation: Let u be a solution to the equation f(u,p) = 0 with
parameters p. To find a solution of f(u',p') = 0 with parameters p' = p + dp,
take u as an initial guess and solve by Newton search.
Even better is quadratic continuation: Take few solutions u for a few values of p,
make a local quadratic approximation to u(p), and then extrapolate to the parameter value
you want to get a good initial guess u(p'). Of course you can do linear, cubic, etc., too.
Jonathon and I did our continuation mostly the poor man's way, with p usually being the
Reynolds number. Sometimes I did linear continuation using the addfields utility.
Jonathan wrote a quadratic continuation utility branchswitch.cpp that tracked a solution
around a saddle-node bifurcation with Reynolds number as the continuation parameter. We also
continued EQBs and POs in cell size (Lx, Lz)
or equivalently (α,γ) = (2π/Lx, 2π/Lz). This is more troublesome because you have to satisfy
the divergence constraint. Typically I would use changegrid to change the cell size and
fix the divergence of the stretched field. The combination of procedures we used was somewhat
cumbersome and didn't help us continue around saddle-node bifurcations in spatial parameters.
Because of these limitations and because I anticipate people in the study group wanting to continue solutions, I wrote a better algorithm that does quadratic continuation in an arbitrary parameter and handles geometric continuation seamlessly. This allowed me to continue EQ1 and EQ2 (Nagata LB and UB, blue in figure) around the saddle-nodes at γ=1.7ish and EQ5 (green) around the saddle-node at γ=2.9ish.
Left as of last fall, Right same fig with new continuations. The figure shows energy dissipation D of plane Couette equilibria as a function of γ=2π/Lz, with α=2π/Lx=1.14 fixed and Re=400. EQ1,2 blue; EQ3,4 red; EQ5,6 green, EQ7,8 black; EQ10,11 magenta.
I have yet to add the continuefields utility to the channelflow distribution and document it.
2009-03-09
We really need continuation studies of our periodic orbits. It was the prominent question at the Newton Institute meeting, and it came up again at my talks at Harvard and McGill and in discussion with Lennaert van Veen. I can do continuation now, with current utilities, but it requires a lot of manual oversight. I would really like to automate the continuation procedure or help someone else automate it.
Here's an example of the problem. We have a periodic orbit solution P19p02 at a given Reynolds
number (Re=400) and given cell size (HKW cell). Let u(Re) be a parameterization of the solution
as a function of Re. We can use u(400) as an initial guess for the solution at Re=390
and Re=410 and then initiate searches at thsoe two Reynolds numbers. E.g.
jg356@pacemaker$ ls Re400/ couette.args data/ orbstats/ orbstats.args P19p02.ff taubest.asc jg356@pacemaker$ grep T Re400/taubest.asc 19.018545664858518 %T jg356@pacemaker$ mkdir Re410 jg356@pacemaker$ cd Re410 jg356@pacemaker$ qsubmit P19p02-Re410 findorbit -orb -T 19.018545664858518 -R 410 ../Re400/P19p02.ff
and similarly for Re400. (qsubmit is a shell function I wrote to simplify
submitting jobs to the PACE job queue). Assuming those searches converge, we get three points on the function u(Re) and
we can start continuingu(Re) via quadratic extrapolation for initial guesses and then solving the nonlinear equations.
E.g.
jg356@pacemaker$ mkdir Re420 jg356@pacemaker$ continuefields 390 Re390/ubest.ff 400 Re400/P19p02.ff 410 Re410/ubest.ff 420 Re420/uguess.ff jg356@pacemaker$ grep T Re390/taubest.asc Re4[01]0/taubest.asc Re390/taubest.asc: 1.8882243932716367e+01 %T Re400/taubest.asc: 1.9018545664858518e+01 %T Re410/taubest.asc: 1.9154708055204622e+01 %T jg356@pacemaker$ continueparam.x 390 1.8882243932716367e+01 400 1.9018545664858518e+01 410 1.9154708055204622e+01 420 extrapolated p(mu) == 19.290731103754673 jg356@pacemaker$ cd Re420 jg356@pacemaker$ qsubmit P19p02-Re420 findorbit -T 19.290731103754673 -R 420 uguess.ff
This is great, and you can even automate the procedure with a shell script, if you keep a fixed steps
in Re. But the trouble is that solution curve starts to change too rapidly and you need to take smaller
steps in Re, or you reach a bifurcation point and have to follow the solution through a turn and go
backwards in the continuation parameter. To do this you have to switch the continuation parameter to
the quantity on the y axis (here average dissipation D) and treat both u and Re as functions
of D be estimated by quadratic extrapolation. All this is time consuming, especially when you have
many solutions to track. So it would be nice to automate it. The AUTO
software system does continuation nicely for low to moderate dimensional systems but it doesn't handle
CFD and Krylov methods.
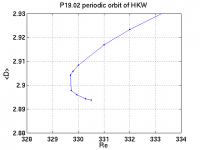
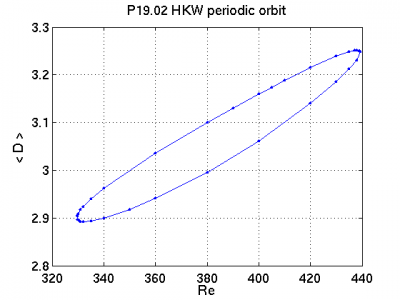
(a) continuation of P19p02 in Reynolds number (b) close-up of saddle-node bifurcation near Re=330 (c) close-up of possible bifurcation point near Re=440
2009-03-11
Managed to complete the continuation of P19p02 in Re via the continuefields, continueparams, and findorbit utilities as shown above. It took a lot of work (running three or four utilities on PACE for each data point), way too much to do for the whole set of periodic orbits in HKW. Last night I wrote a Matlab arclength continuation code that can branch-switch through pitchfork and saddle-node bifurcations. It'll take a little time to reorganize findorbit as a function to be called from a continuation routine, but it'll be worth it.
2009-09-16 Predrag: This is great!
2009-04-06 HKW orbit continuation
Continuation in Re of HKW orbits, via automated continuesoln.cpp. Continuation showed that
- P19p02 and P19p06 are upper/lower branches of same solution
- P31p81, P41p36, and P46p23 have upper (lower) branch partners at Re=400
- P76p85 branches off of P41p36 at about Re=275 in a symmetry-breaking, period-doubling bifurcation.
The dissipation D shown is the mean over the orbit. It would be nice to plot the mean of turbulent simulations as well but this harder to define and compute, due to occasional decay to laminar. We need an escape rate.
PACE is still cooking on these calculations. I'm burning up all the CNS CPUs and quite a few of the other nodes. (2 x 20ish solutions is 40ish computations). Continuation still requires manual intervention now and then. Anyone is interested in using this utility please let me know and I will describe its ins and outs.
2009-09-16
Recently resumed continuation of these orbits for a PO paper, to be produced a.s.a.p., to demonstrate parametric robustness of these solutions. Significantly improved continuation algorithm by restricting continuation point to I-D=0 Poincare section to eliminate temporal phase shift. Contrary to my guess there are still occasional problems with tangency to this section. Below is a portion of the D vs I graph for the P46p23 orbit at three successive Reynolds numbers. You can see that the intersection of the orbit with I=D line goes tangent somewhere between the red and green orbits. My algorithm tries to extrapolate in Re the point of intersection of the orbit with the I=D line, so it gets stuck when the orbit goes tangent to the line. Bummer! Fortunately this doesn't happen very often and there is an easy diagnostic for detecting when you get close to tangency, at which point you can switch to a more transverse intersection. I will need to add this to my continuation code, if I am lucky it will explain a couple stuck continuations I have at the moment and get them going again.
2009-09-16 Predrag: There are 2 or 4 D-I=0 sections. Can't you simply switch search to another section whenever a pair of periodic points (in the section) is getting too close? Typical distance on diagonal to the next periodic point that cycles/pivots around the mean <D> is of order 1, so whenever the next periodic point is on the same side of <D> , distance less than 0.1, simply switch the continuation to the next cycle point?
2009-09-17 JFG: Yes, agreed, switching to a different intersection is the thing to do. My practical question is to what extent right now should I try to automate the switchover in my continuation code, versus simply warning when the condition gets bad and stopping the continuation, and then personally examining D vs I plots, choosing a new intersection, and restarting the continuation. In the long run complete automation will be probably be worthwhile, but I always like to do something manually a few times before trying to automate it, to get a robust sense of the problem and a better idea of the cost of implementing automation robustly versus occasional manual intervention.
2009-09-17 Predrag: Go manual - you want to continue only a few shortest periodic orbits, not all longer ones still to come.
2009-09-19 JFG: Agreed.
2009-09-23
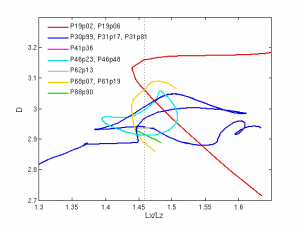
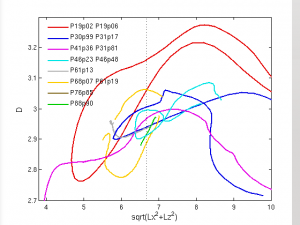
Some new results for continuation of orbits in Re, aspect ratio, and Lx,Lz diagonal. These were generated using continuation on the I-D=0 Poincare section, and temporal integration constrained to the s1,s2 invariant subspace. (So few words, so much work…)
The aspect-ratio and diagonal continuations are still running, as are a couple in Re. Aspect-ratio continuations hold the diagonal sqrt(Lx^2 + Lz^2) fixed, and vice versa. Unfortunately I messed up the way the diagonal was held fixed, so I have to recompute the aspect-ratio plots. Expect that plot to change. I think these results are wonderful; they show us that the short orbits are robust in parameters, and that most of them so far are born in saddle-node bifurcations around Re=320. The orbits are surprisingly robust in aspect ratio and diagonal length. The above plots use mean dissipation on the vertical axis, but even more interesting will be the sum of the unstable eigenvalues or product of the unstable multipliers.
2009-09-25 I determined that Ny=49 is overkill for these computations using resolution.cpp (which reports the magnitude of the largest truncated coefficients and recomputes the solution residual on a finer grid –it is amazing what a difference it make to my daily work to have tools such as this packaged and made easy to use), so I restarted the continuation calculations with Ny=33. But some have not restarted cleanly, indicating other resolution problems, namely in Nx and Nz. Of course changing the box size, as you do in aspect ratio and diagonal continuation will call for changing the resolution. It just happened sooner than I expected. Am investigating, will report mroe later.
2009-10-01
2009-10-01 More continuations. Have determined that P41p36, P30p99, P31p17, and P31p81 are all connected. P19p02 terminates in a Hopf bifurcation at around Lx/Lz=1.6
EQBs in 2pi x 1pi box
In preparation for continuing with pressure gradient for near-wall solutions, I continued some of our alpha,gamma = 1.14,2.5 EQB solutions to alpha,gamma = 1,2 or Lx,Lz = 2pi,1pi. There was really no particular sense to that box. Lx,Lz = 2pi,1pi is no better physically, but it is more conventional. EQ3 does not exist for this box; EQ4 connects to EQ7 near Re=200 instead. I did not try to continue other EQBs. I am trying to divide my work between near-wall solutions, localized solutions, and the I-D=0 Poincare map for the HKW orbits. Could use some grad students.