channelflow.org

08/19/09 I followed the procedure on the howto for finding new equilibrium solutions and like some sort of Christmas Miracle, I found an equilibrium on my first try. The catch is that while it has a little bit of structure (small curls and a streak), the dissipation is very, very, very near that of laminar. I guess I would like a sort of rigid set of guidelines about how to determine whether a solution is a new equilibrium or not so that I don't have to ask on a case by case basis.

08/19/09 JFG: Excellent! Perhaps we should move your table of solution properties to the database for comparisons. Also, I've added some instructions to the findsoln howto and couette for restricting integrations to invariant subspaces, which should help both generating good guesses and searching.

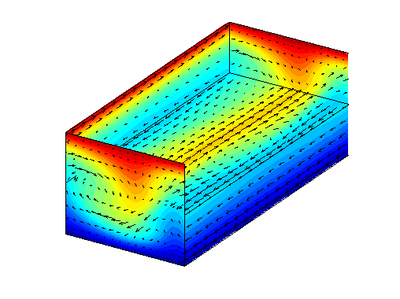
08/19/09 Here is an image of the equilibria that I found that is very near laminar. I leave evaluations of its value up to the channelflow community.

Dissipation: 1

L2IP: 1

Could you post the datafile for the solution and the Reynolds number? I am puzzled. Dissipation = 0 is a suspect value. In our standard terminology the dissipation of laminar is 1, and no solution can have D less than this. L2IP is a bilinear operator on two fields. Did you mean L2Norm? It could be that you found the laminar solution (or epsilon away from it) but the graphing routines scale up the arrows. There is an option in the Matlab plotbox routine to turn off this scaling. Try “help plotbox” in Matlab. JFG 2009-08-18 11:02 EST

08/26/09 Hey John, I just got your email and you are right about the tendency to drift and I actually thought about that last night and resolved that I would work harder and keep rolling a little bit better. The dissipation I listed above is with the laminar removed, so it the solution above does have the same dissipation as laminar. It might be useful to upload the data file for the laminar solution to channelflow, so that one might calculate the distance between nearly laminar solution and the laminar solution and if they are sufficiently close, then they would not be called distinct solutions. I, too, suspect that the above solution is just epsilon away from the laminar solution. I don't think I know how to post the data file, unless it's the same as uploading a .png file. I will try that, and if it isn't that, then please let me know how to do it. I am going to start (today) looking harder for new solutions in different symmetry groups. I also just learned about correlation functions in the Stat Mech II class I have been taking and thought it might be interesting to calculate the correlation functions for all of the periodic orbits we have. I'd like to know what you think of pursuing that idea. It might at least be useful to have a program that can do that. Expect more regular updates from here on out. — Dustin Spieker 2009-08-26 13:26

Hi, Dustin. Thanks for the posting and update. My experience is that the pattern of grad studenthood is a long period of somewhat frustrating, not-exactly on target effort followed by a one or two year burst of intense on-target effort, which happens once you really internalize the problem and own it. The secret to success is getting through the frustrating part fast and having more time for the intense part, by working steadily, keeping focused, and getting help from you adviser. Even if you go way beyond your adviser in your Ph.D., your adviser is indispensable in getting up to speed fast, because there are so many undocumented tricks of the trade you need to learn.

The solution you posted is indeed just epsilon away from laminar. You can test that with the fieldprops utility, which will return various norms and energy norms with the -n and -e option. JFG 2009-08-27 09:39 EST

08/28/09 I've been submitting short jobs to the cluster pretty regularly yesterday and today to try and find periodic orbits in the W03 cell and I had a few comments and concerns:

• randomfield, if fed the same parameters, will generate the same velocity field. This happened for 4-5 consecutive runs before I discovered it.
• Why are there so many more orbits in the HKW cell than in the W03 cell?
• After using randomfield to generate turbulent trajectories, I started perturbing existing orbits to see if the recurrence plots would have more blue spots to search for, we'll see how that works.
• There seems to be a limit of the L2Norm for which if you go below that number, the field is guaranteed to decay to laminar. Any idea what that number is so I can truncate my time integration?
• I'm going to read up and work on confinement to the other invariant subspaces over the weekend.
• Any other tips on generating better trajectories to begin searching for solutions in?

08/31/09 Over the weekend, I have been perturbing the W03 equilibria along their eigenvalues as calculated by arnoldi to generate trajectories and have been calculating recurrence with seriesdist. I am ssh-ing using a computer that doesn't have matlab, so I can't look at the recurrence plots until I get back to Atlanta.

08/31/09 I found something novel today while being unsuccessful at generating good guesses for periodic orbits. I perturbed EQ9 along its first eigenvalue that arnoldi generated, and I might have found a heteroclinic connection between EQ9 and EQ1. I noticed that the recursion plot that I generated looked somewhat different than all the others that I had generated (and I will post it later). When I tried to find an equilibria integrated about 100 steps away from EQ9 along its first eigenvalue, I found EQ1. More on this later…

09/01/09 I have found that being able to find an equilibria from a trajectory generated by another equilibria does not necessarily mean that there is a heteroclinic connection between the two. When I project the trajectory, and the two equilibria on the UB-trans basis, I found that EQ1 does not lie close to the trajectory like I thought it would.

09/02/09 I'm having a lot of problems with “Segmentation Fault” errors on PACE. I'm going to try reinstalling channelflow on the cluster and hope that solves the problem.

What is giving you seg faults? Can you uote the exact command you ran and provide the input files if any and the output? Fixing it might be as simple as commenting out the “fftw_cleanup()” function in the top-level channelflow program, which I have found to produce seg faults, for reasons I can't fathom. But this function is purely a nicety and can be eliminated. Agreed that finding an EQB from a guess on another EQB's unstable manifold does not imply a heterclinic connection. JFG 2009-09-02 14:16 EST

09/02/09 I don't know exactly know what was causing the segmentation faults. I was integrating an initial condition, and when I tried to take L2IP or L2Dist or fieldprops on fields after u1.ff, I got a segmentation fault. I reinstalled channelflow and I haven't had the problem since.

randomfield has a -sd or –seed option to change the seed of the random number generator. JFG 2009-09-06

09/08/09 Wasn't very productive, computationally, today. The cluster is getting maintenance tomorrow and so jobs could only be scheduled up to an hour long which isn't very useful for the calculations I want to do. Last Friday, John G. and I talked about difficulties I was having with finding periodic solutions which included:

• Unable to generate random initial conditions that didn't immediately decay to laminar,
• Possible periodic solutions just falling onto an equilibrium and slowly revolving a negligible distance from that equilibrium.

So today I wanted to start working on finding periodic orbits in [4π,2,2π], [2π,2,2π], and HKW, and continuing those to see if they could be linked up with periodic orbits in the other boxes. These boxes sustain turbulent trajectories for longer periods of time, and therefore should generate more good guesses for periodic orbits. Because of the time restriction, today, I couldn't even complete a seriesdist calculation to look for good guesses, but tomorrow after 12:00 PM ET, that will change.

09/08/09 I got a few references from John G. on Friday about what the numerics of channelflow are based on. I really want to know how the pressure gradient term works and how it is calculated, so I am going to check those books out. The books were a series by Canuto and Hussaini, and the following I can check out from the GATech library:

Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamics (2007)

- and -

Spectral Methods in Fluid Dynamics (1988)

09/10/09 I checked out Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamics and after a brief perusal, I learned that more than a brief perusal will be needed to understand what is going on.

09/08/09 John G. and I talked about perturbing all of the equilibria about imaginary pairs of eigenvalues like we did for the Upper Branch equilibria, in hopes of finding periodic solutions that lay on the unstable manifold of the equilibria.

09/09/09 I started 8 or 9 periodic findsoln's going, a couple (3 or 4) in the [4π,2,2π] box and more in the HKW box. The HKW box has generated better guesses so far, in that findsoln didn't bail out after 1 hour, but instead are still running. I made a randomfield in the [4π,2,2π] box, integrated it a large number of steps, and then looked at the recurrence plot for the trajectory. For the HKW cell, I wrote a script that found the eigenvalues of the HKW equilibria, then perturbed the equilibria by the first eigenvector and integrated and then looked at the recurrence plot. For EQ4, and EQ9, this blind approach worked well, and I was able to get 3 guesses out of EQ9 and two out of EQ4. I am also searching for an equilibria based on a guess generated in the same manner by EQ7 in the HKW cell.

I should also be able to fish a little bit more and hopefully I will know by then if any of my current searches have been fruitful.

09/09/09 John G: I was wondering if it was okay to start appending properties of the equilibria onto the appropriate places in the database. I kind of feel like that area is off limits to editing unless express written consent is given.

9/11/09 It looks as though, one of the guesses I made in HKW cell is converging to a periodic orbit. Currently, the L2Norm(G) is at 1.1E-13 and the Period T = 97.4264, probably making it a new periodic orbit. I should know in a few hours (hopefully) if it is an official new periodic solution. This one was found by perturbing EQ4 in the HKW cell by its first eigenvector (which forms an imaginary pair with ef2) and then integrating. Perturbing solutions by imaginary pairs of eigenvalues, so far, seems to be a good heuristic for generating good guesses for periodic searches. — Dustin Spieker 2009-09-11 08:30

T = 97.4264

09/15/09 Over the weekend and at the beginning of this week, I've tried perturbing the W03 equilibria by imaginary pairs to see if my heuristic (as mentioned above) would produce in the W03 cell. Out of the 7 equilibria I tried this on, I was able to generate 4 good guesses and I am watching those to see if any of those will produce periodic orbits in the W03 cell. I also started continuing my periodic orbit in Re, Lx, and Lz and calculating its eigenvalues today. I gave the continuations 6 days to run and I expect to get the eigenvalues back in about a day or two. I am leaving the projection plot up to John G. as he already has the rest of the orbits projected and will be more expedient at being able to produce a comparative plot. — Dustin Spieker

09/15/2009 Problem: In wanting to keep the most updated version of development codes in channelflow, I have been advised to quit using tarballs and start using svn. The only problem is, I do most of my computing on the cluster, and as far as I can tell, PACE doesn't have any of the svn scripts that I need in its bin. I've tried to go through the steps in CNS Subversion, but that hasn't helped so far. Can anyone out there help me with setting up a repository on my PACE account?

09/16/2009 Predrag's solution: I put the answer here here, so other people can find it more easily.

09/19/2009 John's solution: Channelflow is hosted at http://svn.channelflow.org, so you can access it directly with svn commands from anywhere on the intertubes, rather having to ssh tunnel to zero through the ssh.physics.gatech.edu. See the Installation instructions.

09/15/09 I have decided to work on finding equilibria and periodic orbits on other isotropy groups. I think I'll have more to say today, but right now, I have writer's block, so I'm gonna set some more stuff up.

09/16/09 Predrag: I suggest -for now- 50% time on finding equilibria and periodic orbits, 30% on studying literature (and blogging what you learn while you are learning it) 10% on Itano and 10% on unstable manifolds/Poincaré sections (which is what we need to do if we want to revolutionize plumbing instead of just repeating what everyone else does). To be fine-tuned as we go along…

09/17/09 I am guessing that the best place to start my review of the literature is at the chaosbook library, and that is where I will start. I successfully used svn.channelflow.org so that I might develop my own channelflow codes. I initially had trouble compiling but it was a mere path problem that I fixed. I think my file structure on the cluster needs a little work. More later today, hopefully.

09/21/09 P19p02 and P19p06 are connected via continuation in Lx. Here are JFG continuations in Re, where continuation showed P19p02 and P19p06 are upper/lower branches of same solution.

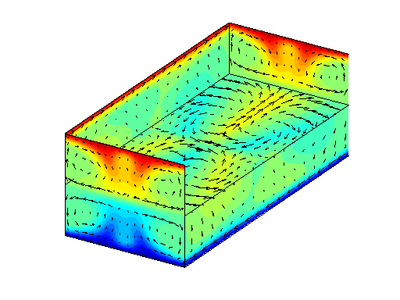
09/24/09 I found an equilibria in the W03 cell that is s3 symmetric, but not entirely symmetric about s1 and s2. It's dissipation is 1.603438 and its L2Norm is 0.24051, which I think qualifies it as sufficiently distinct from the other known equilibria. I'll post an image and data file by the end of the day.

dat file

I'm convinced this in not a new equilibrium. It looks no different than the EQ1 S-invariant equilibria. I generated an initial guess by creating a random field that was s3-invariant (but not invariant under actions of s1 or s2) with the following command:

     randomfield -Nx 48 -Ny 35 -Nz 48 -s3 -sd 4 -a 1.14 -g 2.5 ustart.ff

I then integrated the field in the s3-symmetric subspace using the following command:

     couette -T0 0 -T1 600 -sy s3.asc -u 0.06 ustart.ff

with s3.asc looking like:

     %1
     1 -1 -1 -1 0 0.5

I looked for regions where the velocity field didn't change much in time using the seriesdist function and came up with a good guess, a guess that led to findsoln finding the above data file. I became suspicious when I found another solution using the same method as above but with a different seed integer in the randomfield command. It too looked like EQ1, but it had a dissipation of 1.7629 instead of 1.603438 or 1.42. They also all had distinct L2Norms. Can anybody shed some light on what I am doing wrong?

09/25/09 JFG: I downloaded and examined the solution you posted above, and it looks like a new solution to me. Good job! I wouldn't put too much weight on the visual appearance of the solutions. We've seen several cases where the solutions are hard to distinguish visually. This particular solution looks a lot like EQ1 but has weaker symmetry (s3 only). It might turn out to be as important as EQ1. I am curious about its eigenvalues, and those of the other solution you mention. Really great…

P.S. I have also verified the P97p43 periodic orbit of HKW that you found.

09/26/09 PC: Wunderbar!

09/28/09 Here is another candidate for a new solution using the same method as listed above. You might see now why I am skeptical as to whether or not these are new solutions.

dat file

Domenico gave me a 45 minute talk today about his project and I thought it was really interesting. Along with the reading I've been doing in chaosbook, I've really begun to understand the importance of Poincare sections and return maps. It seems kind like the starting point for periodic orbit theory. I learned today that we are a long way away from feasibly using the Fokker-Planck equation toward our project. I've been wanting to blog a little bit about what I've read in chaosbook; should I put those questions/comments in the chaosbook blog or in my blog? Kind of like Plato's shadows on the wall, its taking me a little bit of time to digest everything I've read and try and put it into cogent thoughts, but I will start blogging about it soon.

09/28/09 PC: For me the learning never stops - every time I revisit it is from a different angle. And I cannot believe how I missed to see the angle the last time, and how slow I am in learning how to do the next thing.

Start writing in the ChaosBook blog - the idea is like asking questions in a lecture, usually one is not the only one who missed it, and it helps us all. Try it, we can always move stuff to your blog later, if that feels more appropriate.

09/28/09 Eigenvectors for the new 'equilibria' should be done computing by tomorrow sometime.

It seems to me like the vector fields prefer to be symmetric in all s1, s2 and s3. On a number of the runs I have performed, where I integrate an initial condition that is only s3 symmetric, the trajectory quickly tries to become s1, s2, and s3 symmetric. Is there a reason for this?

09/28/09 PC: I think only the laminar equilibrium is invariant under s1, s2 and s3 (might be wrong, would have to recheck our paper on equilibria), so it probably means that your state is decaying towards the laminar state.

09/29/09 JFG: Most of our equilibria satisfy s1,s2, and s3 = s1 s2 and most of our work so far has been in the S subspace defined as the set of fields satisfying these three symmetries. Your observation that u(t) tends towards S (for small boxes, and modulo phase shifts) accords with my own –some time ago I did some studies involving initial conditions with no symmetries and observed that they quickly came close to S (or a translation of S), with decomposition into S-invariant and S-noninvariant components of, say 0.98 and 0.02 (e.g. L2Norm(P_S(u))/L2Norm(u) = 0.98). I don't think anybody understands this better than this: s1 symmetry matches the spanwise-alternating stripes of fluid flowing +/- along the x streamwise direction. s2 symmetry matches the sinusoidal wiggles of these stripes along x. The stripes are closely related to the most slowly decaying eigenmodes of the laminar solution (rolls), and the wiggles are closely related to the dominant instability of the stripes. It would be great to understand the attraction of S better, for example, by showing in general u(t) is more drawn to S-symmetric solutions by eigenfunctions pointing into S than expelled away from S by those pointing out of it.

BTW, I have added your recent equilibria to your table of EQB properties as EQ14 and EQ15. I believe they are distinct solutions even though they look familiar. I trust the norms and symmetry measurements better than my eyes.

09/30/09 PC: John is right, G_S = {e,s1,s2,s3}-equivariant subspace is where most fishin' has taken place so far, and John's simulations in the full space always hug it closely. What I was referring to is the full symmetry group G of plane Couette - laminar equilibrium is the only solution in Fix(G). I hope it will become clearer once we quotient the symmetry. In the Kuramoto-Sivashinsky this has revealed surprises, such as a traveling wave that we hitherto thought isolated playing important role in organizing the dynamics.

10/01/09 JFG: Yikes, another month is upon us. The P97p43 orbit you posted is on a slightly different Wally-style HKW geometry, alpha, gamma = 1.14,1.67 a.k.a Lx,Lz = 0.877193,0.598802, compared to the slightly different Lx,Lz = 0.875,0.6 geometry used by the original HKW paper, Viswanath, and our other HKW orbits. I have continued the orbit to the latter HKW box in a few steps; there its period is T=96.66. The number of The Beast is appearing with disturbing frequency in our research, here, and HKW's sqrt(Lx^2 + Lz^2) = 6.66. Dare we continue?

10/01/09 PC: We have no choice but to work for the Devil. With our publication rate She is our only hope. Does P97p43 ⇒ P96.66p666 have a room of her own in the state space projections, or is closely married to a known suspect?

10/02/09 T=59.86. Sorry I generated these in a slightly different box, I have gotten used to using alpha and gamma as opposed to Lx,Lz. Should have at least one new W03 solution today.

10/02/09 JFG: No problem, I'm sure I advised you to use alpha and gamma over Lx,Lz; unfortunately I had already computed twentyish orbits in Lx,Lz = 0.875pi, 0.6 pi before converting to that myself. By the way, did you notice that your P59p86 orbit is s3-symmetric but not s1 or s2? Regarding state-space projections of orbits, my motivation for that with these orbits is pretty low, after spending a lot of time futzing with semi-reasonably motivated basis sets and producing lots of figures but not getting anything concrete out of it, just nice-looking pictures. In the narrower box with lots of EQBs the state-space portraits got us heteroclinic connection; for HKW orbits, nothing so far. For distinguishing one orbit from another, I vs D is simple and not bad.

10/02/09 I did know that this s3 symmetric but not s1 or s2. I more or less intentionally tried to find one with that property. Just from reading, I don't understand what you're not motivated about, projecting –or– finding orbits with symmetry comparable to p59p86. The equilibria that I thought I was going to find in W03 was just EQ12.

10/02/09 JFG: I'm not motivated to project make more state-space projections of orbits like this. Maybe if we figure out a more intelligent approach. Maybe there's a good way to project the I-D=0 surface and look at the unstable manifolds of the return map.

10/07/09 DWS This is the last time I will post a solution that isn't the correct box dimensions - I promise. I just have a script that I haven't edited yet that generates some good guesses but only a few good guesses ever converge to anything so I don't change the script for some reason. T = 65.72 I will continue it to the correct box size, just letting everyone know it is there.

Does anyone know what I can do if I restarted my Linux machine and everything on the screen becomes huge? I think the resolution of the screen went down and it looks like I can't change it. Is there anything I can do or do I need to reinstall because huge icons and only half of an accessible Desktop are getting really annoying.

Afraid to ruin the feng shui of the chaosbook page, I will avoid making a new thread on cycle stability and post my questions here:

Are the eigenvalues that we calculate and generate using arnoldi iteration in PCF usable in Floquet Theory discussed in Chapter 5 of chaosbook. Using arnoldi, we generate 10-30/60000 eigenvectors and eigenvalues. How many do we need to use some of the tools discussed in the latter half of Chapter 5.

10/07/09 JFG: I found a T=65.53 orbit in Lx,Lz = 1.75 pi, 1.2 pi ; maybe this is the same as your T=65.72 at alpha,gamma = 1.14, 1.67. By the way I left off a factor of 2 in Lx,Lz in my 10/02/09 note and have just changed that now. For your Linux desktop, if you are running KDE desking try resetting your screen resolution with the “krandrtray” application. If youre' running Gnome, I don't know what the corresponding application is.

I wouldn't worry about futzing the feng shui of the chaosbook discussion pages. That's what they're there for. In answer to your question, yes, the eigenvalues of a periodic orbit computed by Arnoldi iteration are the same as the Floquet multipliers in Chapter 5 of chaosbook. Arnoldi iteration is just a convenient way to calculate them. Your second question is the $64k question of dynamical systems and turbulence: how do we carry over the ideas and techniques of chaosbook to systems for which we can't write down a fundamental matrices or Jacobians (because the dimensionality is too large), but instead can only calculate numerical approximations to trajectories u(t) and a relatively small set of leading eigenvalues and eigenvectors? In principle, ti should be easy: only the leading eigenvalues are important. In practice, 99% of the work is in figuring out how to throw away all the other directions that don't matter.

10/08/09 It looks as though the T=65.53 orbit you found is the same as my T=65.72 orbit. My continuation has the period at 65.5377 right now and the most recent dT was -2.469e-05. If it is the same orbit, could that suggest that it is an important orbit? I did notice that the factor of 2 you left out when I started getting f^t(u) not finite errors. I also guess I missed out on the reason for the choice of the I-D=0 for recent continuations and other calculations.

10/08/09 JFG: I get T=65.5392 and mean dissipation D=2.935 at 48x33x48 and T=65.5345 at 64x49x64. At 48x33x48 I have come to expect 1e-04 resolution at best, so quantities such as T can vary on that order depending on which point on the orbit is your starting point. My main reasons for going ga-ga over I-D=0: its simple, all orbits pass through it, all EQBs and TWs lie on it, and it eliminates the free choice of temporal phase. Things not so great about it which I am ignoring or working around on a case-by-case basis: (1) D is a nonlinear function of u, so the section is a curved surface in the space of spectral coefficients, (2) some orbits pass through it several times, and in such cases any particular crossing could go from transverse to tangent and then disappear under parameteric continuation. I have added a -poinc option to findsoln and continuesoln to restrict searches and continuations to the I-D=0 Poincare section. That code is in channelflow svn. Another utility (not in svn yet but you might have a copy) integratePoincare will integrate u(t) and output any crossings of the I-D=0 section. You can use the output of that on a periodic orbit as a starting point for a findsoln -orb -poinc search. If you find the I-D=0 points for your new orbit, it'll be easy to compare your data point with mine, precisely. BTW, I focus on d(I-D)/dt < 0 crossings, as these are generally closer to the laminar EQB than d(I-D)/dt > 0. There are quite a few interesting things we can more simply now, with this section, like extending the unstable manifolds of the return map around orbits, seeing which orbits are clustered together, which are isolated, what transitions are likely/unlikely, etc.

10/09/09 PC: For me the most important virtue of I-D=0 section is that is G-invariant, so it will work equally well for relative equilibria and relative periodic orbits and unstable manifolds, when we get to that. That it cuts every periodic orbit at least once is great, and it has to cut longer periodic orbits n times - it provides a coarse symbolic dynamics already. The tangencies as one varies Re do and must arise, and make applied mathematicians feel good, but that is not what we need in order to develop a theory of moderate Re boundary wall-bounded turbulent flows.

Our task is to fix Re and show that we can describe important unstable coherent structures observed and their dynamical relations (can I get from her to there, and how fast?) at a given fixed Re and given geometry and boundary conditions. In long run we will most likely need a number of invariant Poincaré sections (“local charts”) to get the partitioning of the state space right, but I-D=0 section will be easy to sell to the community because it is physical: the points on it represent instances when the drag is exactly balanced by the bulk dissipation, the most physical section, independent of one's particular implementation of dynamics that I am familiar with.

Also JFG's “focus on d(I-D)/dt < 0” remark is important; if you study the sequence of Lorenz examples in the ChaosBook, you will find the section above the Lorenz equilibrium EQ1 very convenient, while the opposite direction flow below EQ1 very inconvenient.

10/09/09 JFG: Good point about I-D=0 being G invariant, it wouldn't be good without that. And nice trick using // ... // to get short expressions in italics! I agree that exploring dynamical relations at fixed parameter values is the thing to do, now that we have a large set of orbits and a good poincare section. We could start by exploring perturbations within the unstable manifold of a single orbit / fixed point (FP) of the Poincare return map. Choose one that has just a couple not-too-strong unstable eigenvalues and comes up frequently in searches (and so is likely to be dynamically important), start integrating small perturbations, build up an approximation to the unstable manifold (within I-D=0), plot projections onto a plane aligned with eigenfunctions, determine the radius around the FP in which linearized dynamics are accurate, compare that to the distances to the nearest FP from other orbits. Keep at it and see if you can build up a transition network among the FPs. All the tools for this are in place, except Arnoldi iteration within Poincare sections, which is written and running but is giving results I don't entirely trust (the unstable eigenvalues come out ok but it produces too many marginal). I think it's a minor thing, just haven't had a chance (or need) to focus on it and figure it out. Still, for now you could use eigenfunctions of the fixed-T map (which arnoldi.cpp does reliably by default) as initial small perturbations and get their intersections with I-D=0 using the Poincare-map integration code.

10/13/09 DWS T=59.77 Here is the continued solution that I found above in correct (lx, lz) = (0.875,0.600) cell size. I started ~10 searches for new periodic orbits today and hope to start a few more by the end of the day. I haven't started using the new code provided in my most recent checkout of svn.channelflow.org. I am encountering some compilation errors of the programs-devel file that are arising from the funky way I set up my PACE file system and I will need to fix that before I can start using the I-D=0 section.

10/15/09 DWS The last couple of days I have been initiating many searches for periodic orbits in the HKW cell. I have come up with a fairly efficient way of generating turbulent trajectories that don't decay to laminar all that quickly. I find the recurrence plots are the best tool for me, so far, for visualizing the trajectory of the flow. One thing that has really begun to strike me during these searches is the how it seems that the periodic orbits shepherd the flow. The recurrence plots have shown a couple of times that the trajectory will stay close to one periodic orbit for a significant amount of time then goes to the neighborhood of a periodic orbit for another significant period of time. I have refound orbits T=75.35, T=76.85, T=87.89 in my most recent searches, 15 of which I started.

10/16/09 PC Staying close to one periodic orbit for a significant amount of time is not expected, as the lifetime in the neighborhood is proportional to (weird positioning of this formula implies that my “how to blog LaTeX” post does not work, quite, would need to edit css files apparently). If it does hang around one expects the most unstable Floquet multiplier to be small, and that periodic orbit to play an important role in the ergodic dynamics. I guess you will compute the Floquet exponents/multipliers for the new periodic orbits?

John found it useful to keep track of how many initial guesses went to which orbit - though the numbers are small, this statistics gives you some sense of relative importance of different orbits. Newton method does not have much to do with what the dynamics does, but still it is something.

10/16/09 JG The Newton-Krylov-hookstep search algorithm we use is not Newton until it gets close enough that linear approximations are valid. Prior to that it is a gradient descent. So it does not bounce around the search space randomly like Newton search, when far away from a solution. It always creeps downhill towards a better solution, never going farther in one step than warranted by curvature at the current point. The convergence region of the Newton-Krylov-hookstep algorithm is the simply connected region surrounding the solution and bounded in all directions by the surrounding local maxima of the residual |f^t(u) - sigma u| (i.e. if it rains on the search space x residual, the watershed of the solution). It's not the crazy Julia-set convergence region of the Newton algorithm.

Early on with dokuwiki I tried a few of the things suggested on the web for correcting the in-line Latex alignment, but couldn't get them to work. So I settled for using simple ASCII for inline math.

10/16/09 DWS Working on the floquet exponents/multipliers of the new periodic orbits. I wanted them to be in the correct size boxes before I calculated them. As far as the the equilibria go, here are their first 10 eigenvalues.

10/20/09 PC There is no point doing these tables in dokuwiki format. You need them in your thesis, and John and I have to agree on how to present periodic orbits in our periodic orbits paper, so I have toiled away for past two days on a proposal how to tabulate them. DWS, JFG, ES, and RLD, please check out ChaosBook.org section B.3 Eigenspectra: what to make out of them?, and lets skype / blog / discuss how to do present these results.

10/20/09 PC Dustin, we have to (re)activate your svn LaTeX blog, both to compile there your eigenvalue tables in a publishable and/or thesis format, and for you to systematically write down stuff you are learning and reading. I know you are computing, and that is great, but I also have to know what theory you are learning as we go along, to help you learn what you need for this project. I will recheck the state of your LaTeX blog, and then help you get started.

10/20/09 PC Dustin and John, are the eigenvectors such as UB eigenvectors the Gram-Schmidt orthogonalized ones, or are they Floquet, non-orthogonal `covariant' eigenvectors? We need only the Floquet eigenvectors, the Gram-Schmidt ones have no dynamical significance, except for the first one/pair (see the discussion in the Siminos blog).

10/27/09 JG They are non-orthogonal Floquet eigenvectors.

10/29/09 DWS After reading most of John H.'s Thesis appendix on Symmetries in PCF and I believe I finally got a good grip on how to generate vector fields that are in certain isotropy groups. I guess I would like someone to check that the generators that I am feeding to channelflow are in fact the correct generators:

S3.asc

  %1
  1 -1 -1 -1 0 0

R.asc

  %2
  1 -1 -1 -1 0 0
  1 1 1 -1 0 0

Rx.asc

  %2
  1 -1 -1 -1 0 0
  1 1 1 -1 0.5 0

Rz.asc

  %2
  1 -1 -1 -1 0 0
  1 1 1 -1 0 -0.5

Rxz.asc

  %2
  1 -1 -1 -1 0 0
  1 1 1 -1 0.5 -0.5

I'm pretty sure S3.asc, R.asc, and Rx.asc are correct, it's the Rz.asc and Rxz.asc that I am concerned about.

10/29/09 JFG: R, Rx, Rz, Rxz are all fine but S3 should be

S3.asc

  % 1
  1 -1 -1 -1 0 0.5

I am going by the definitions of the groups in Gibson, Halcrow, Cvitanovic JFM 2009, eqns 3.3 and 3.11, since I get only a half-written version of Jonathan's thesis from SVN (what's up with that?). There S3 = {e, s3} = {e, σxz τz}. This definition is conjugate to yours under a quarter-cell shift in z. Note that our work has focused, for historical reasons, on S = {e, s1, s2, s3} as defined by eqn 3.3, but that it might be better for simplicity and consistency to switch to Rxz, which is conjugate to S. Then R, Rx, Rz, and Rxz are all 'lined up', i.e. built from the same set of generators and symmetric with respect to the same choice of origin. If you stick with S rather than Rxz, you should determine the conjugate versions of R, Rx, and Rz that have s3 = σxz τz as a generator rather than σxz. Unless I have lost my touch for fiddling with symmetry groups, those are the left-hand-sides of

{e, σxz τz} x {e, σz τz} ≅ R
{e, σxz τz} x {e, σx τx} ≅ Rx
{e, σxz τz} x {e, σz}    ≅ Rz
{e, σxz τz} x {e, σz τx} = S ≅ Rxz

which I got by applying the conjugacy rules discussed on page 6 of the above paper.

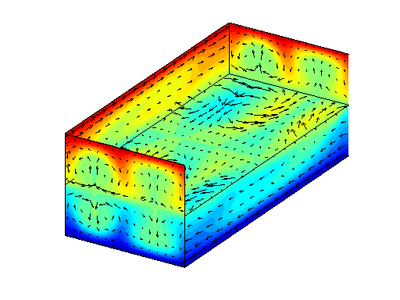
10/30/2009 DWS Found a new equilbrium EQ16 today using S3 = {e, σxz} as one of the generators of the R isotropy group instead of S3 = {e, σxz τz}, not that I am condoning this behavior. It's dissipation is 3.492 and its L2Norm is 0.333.

Data File

10/31/2009 PC That's great. For each new equilibrium one also needs eigenvalues, and needs to place it into the Gibson-style state space plot, to see where it belongs. While copying the 3D portrait to your LaTeX blog I noticed that you did not crop away the white acreage around the figure, and it was bigger than needed - just by cropping it in gimp I reduced its size form 220MB to 90MB. If you follow formating preferences and how to post a movie, it will save time in preparing thesis/articles version.

10/30/2009 DWS I am currently reading about the isotropy groups in Halcrow's thesis so that I can write down the isotropy groups of the eigenvectors of the periodic orbits I have found. I feel like I need a better understanding of group theory to continue on in this project, so at first I looked in birdtracks.org, and I had no idea what was going on. I then asked Domenico what he thought the best path of learning would be for me and gave me his copy of Group Theory and Quantum Mechanics by Tinkham, and told me to read chapters 2 and 3.

10/31/2009 PC I like Tinkham. He does finite groups very ellegantly, in a few pages, and you can check all the algebra. He'll make you feel good. Of course, then it takes years to really understand it. birdtracks.org has a totally different, high-energy audience, and is not useful to the dynamical systems user. I recommend reading World in the mirror in parallel - it's what you will actually need, I've been writing it with plumbers in mind.

11/02/2009 JFG What is the symmetry group (or the complete set of generators) for EQ16? Is the group {e, σxz τz} x {e, σz τz} or {e, σxz} x {e, σz τz} ? The former is equivalent (conjugate) to R, the latter to Rz. About figs, I disagree with Predrag on this. You will probably produce several hundred figures for your blog and only a large handful of these will make it into your thesis. Making all those figures conform to formats designed for other purposes is inefficient. About group theory textbooks, if you get the sense that the explanation is getting top-heavy in formalism, that's a good place to stop.

11/02/2009 DWS I actually used the generators of R = {e, σxz} x {e, σz}, (as per Halcrow's Thesis eqn. 118) to generate and integrate the initial condition, but I didn't constrain the search to any isotropy group. I hope to be able to quickly determine isotropy groups after learning some more elementary group theory. The symmetry that I can quickly read out is {s1,s2,s3,r1,r2,r3,tx,tz,txz} = {0.87,0.84,0.80,1,1,1,0.87,0.80,0.84}.

11/02/2009 JFG Ok, that's good. You can see both of the σxz and σz symmetries by eye. here is a channelflow utility for determining the isotropy groups of a solution: findsymmetries. It works best if the field is already aligned as best as possible with the z and x,y symmetries about the origin or middle. You can (almost) do that easily with symmetrize, which translates in x and z to center the field best for s1 and s2 symmetries. It would be a small change or addition to enable symmetrize to optimize for σxz and σz symmetries as well.

11/04/2009 DWS Initially I used the findsymmetries command on the new equilibrium:

  findsymmetries eq16.ff

which yielded

  1 1 1 1 0 0

which, if I'm not mistaken, is only the Indentity. So I used the symmetrize command on EQ16, and repeated using the findsymmetries command:

  symmetrize -s1 -s2 eq16.ff eq16max.ff
  findsymmetries eq16max.ff
      1 1 1 1 0 0
      1 1 1 -1 0 0
      1 -1 -1 1 0 0
      1 -1 -1 -1 0 0

which I think are just the discrete dihedral group {e, σx, σz, σxz}, with none of the continuous symmetries of G_{PCF}. Does this calculation seem to be producing obvious results or is what I did something worthwhile?

11/04/09 JFG Totally worthwhile. I downloaded eq16, repeated the calculations, and got the same results. The symmetry group of this equilibrium doesn't appear to involve any translations. Since you started the search in this symmetry group, it makes sense. This is very, very good –our first equilibrium in this particularly simple subspace. We have some crude idea that S is the most important subspace but we don't know why, exactly. Understanding the dynamics of other subspaces should help answer that question. Here's a picture of the xz midplane.

By the way, applying symmetrize -s1 -s2 to this field works only by happenstance. The symmetrize is currently hard-coded to handle s1 and s2 symmetries, with those options. It would be better to revise it to load symmetries in from a file. Then you could find the optimal translation for any given symmetry (with a caveat or two, namely that as stands it optimizes x and z translations separately). Also, note that the output of fieldprops -sy is the fraction of energy of the field in its symmetric and antisymmetric components for the given symmetry. 1 0 indicates u is symmetric in s, 0 1 indicates antisymmetry, anything else indicates the field is neither symmetric nor antisymmetric in s. In more detail, let P_s^{+/-}(u) = 1/2 (u +/- s(u)) so that u = P_s^+(u) + P_s^-(u). The numbers reported by fieldprops -sy are |P_s^{+/-}(u)|^2/|u|^2. Since the projections are orthogonal the sum of the squares is 1.

11/04/09 PC According to what I have read, see equilibria_of pCf with_one_of_the 5 isotropy_groups, Tuckerman & Barkley have found a R-isotropy solution, but in a different context, this is the first one within the small-cell setting we have been exploring. Congrats!

We do not have any Rx-isotropy or Rz-isotropy, though Schmiegel has a load them with Rz-isotropy. So if you want to go on fishin', I think you have the best chance to nail one of Rz-isotropies. Filling out this puzzle would be nice, as we never understood why Rxz-isotropy is physically the most important. Waleffe's physical intuition tells him that - his arguments are someplace in Gibson's LaTeX blogs which are a bit hard to navigate. I feel more comfortable with a cold-cut calculation than with much intuition…

As always, one needs the eigenspectrum, and see where the quartet of these equilibria fits into Gibson state-space projection. Some of equilibria might be quite a ways from the ergodically connected component, one never knows.

There might also be some important relative equilibria - in Siminos thesis it turned out that they are much more important in organizing the attractor than what we had expected.

You might try to check out svn gibson, I do not remember whether I gave you the access, but I did generate a contents page for all his blogs combined, there is lots of interesting stuff there that you might enjoy reading.

11/06/09 DWS I realized last night that my generators were incorrect and that finding EQ16 was a happy accident. I discovered this when I was finding S-invariant solutions when I thought I was confining my search to the Rx-invariant subspace. I have since made the appropriate changes to my symms files so that they match the outputs of the findsymmetries command.

Finding equilibria in the other fourth order isotropy groups is proving somewhat of a chore. Firstly, when I generate a random field to integrate, I have to give the random field a little more ummmffff. In order to keep the trajectory from instantly going laminar, I have to give the field a Norm of .35 instead of the default .2. This leads to the problem of creating divergences in velocity field that confuse the computer, so I have to use a time step about an order of magnitude smaller than the default.

Just found an equilibrium that satisfies the following group of symmetries: {e, σx, σxτz, τσxz}. It must be conjugate to one of the other 4th order isotropy groups. It has a dissipation of 2.97947 and ||u|| = 0.291661.

Data File

11/08/09 PC About EQ16 - it has high dissipation rate, and it has most unstable directions, closely spaced, that I remember ever seeing. We might want to list for all equilibria: (1) the sum of positive eigenvalues - a measure of how unstable an equilibrium is, and (b) all eigenvalues to Kaplan-Yorke cutoff (if you add next contracting eigenvalue, the sum becomes negative). Also, I think you need to continue EQ16 to lower Re, see when it is born, and who's its partner(s). It might be that the whole subspace is forced to have so many wiggles by the symmetry that it does not play a dynamical role at Re=400.

11/09/09 DWS I'll should be able to calculate the above-mentioned quantities for most of the equilibria (I don't have a list of eigenvalues for EQ9-EQ13. I also found out that EQ17 is a member of isotropy group R after I shifted the solution by .25*Lz. Continuing these equilibria is proving somewhat of a chore. I'll post plots illustrating what I mean, but the equilibrium doesn't seem to be a lower or upper branch of any other equilibrium in the R isotropy group. I've been continuing EQ16 in the restricted R isotropy group, only. I can say that the equilibrium seems to have a lower bound of approximately Re=259.

11/09/09 PC Re=259 sounds good. But it cannot be born out of nothing - either comes with a partner, or it has bifurcated off something with a larger isotropy group.

Bad news on the group theory front - I might have to call a set of symmetries of a periodic orbit its stabilizer. Yet another ugly word where “symmetry of a solution” would suffice. Will keep you posted.

11/09/09 DWS Okay, so it looks like EQ16's partner is EQ7, I'll be more certain when the continuation has actually reached Re=400. On the tabulation of the sum of the positive eigenvalues, I only counted one in a pair of imaginary eigenvalues, is that acceptable? Also, when I'm figuring out the Kaplan-Yorke cutoff, should I be providing the index of the eigenvalue, i.e. what am I providing there?

11/10/09 JFG Insomnia strikes. A number of small sticking points for me in the above few posts: (1) EQ17 just a few entries above is a typo for EQ16, right? Also, there must be one or more typos in the symmetry group you listed for EQ16: {e, σx, σxτz, τσxz}. The last element doesn't follow our notational conventions and isn't the product the previous two elements. But the product σx σxτz = τz is not one of the symmetries of EQ16, judging by the image of it above. (2) If EQ16 is in R, it's unlikely to be connected to EQ7, which is in S ≅ Rxz. Besides, I have continued EQ7,EQ8 up to Re=400 and the upper branch drops back to D≈1.8 by Re = 400. See the EQB-TW JFM, fig 10. (3) In your discussion of problems with needing more umph for time-integrations in subspaces other than Rxz, did you really mean that you encountered problematic divergences? Or was it really problematic CFL numbers? I would expect big CFL numbers in the circumstances you describe; big divergences would be some cause for alarm regarding the code. The randomfield utility has just two tunable parameters for producing random velocity fields: smoothness and magnitude. You can probably avoid the problems you've hit by increasing the smoothness parameter. Or, starting new “random” trajectories by perturbing u from a previous simulation in the desired symmetry group. Multiplying a u by a constant or constructing a linear combination of several us should do.

At least “isotropy” has straightforward etymology in Greek. In retaliation for the misappropriations physics terminology I think I will start using terms from mathematics to describe concepts in physics. For instance, I'll call projectile motion “differentiation” and condensed matter physics “descriptive set theory”. That'll show 'em.

11/10/2009 DWS (1) I don't know if I made a typo, but I have found a 17th equilibrium, and from the continuation of that equilibrium, I will soon have an 18th. (2) I thought, based on Halcrow's thesis, that EQ7 was in an eighth-order {e,τxz}xS, not just S, but I do think that the continuation I performed is in error and I don't know why. I'll put up my exact string of calculations today, I've got an appointment here at 10. (3) You are right about the CFL numbers. I don't feel there is any divergence being caused by the code.

11/10/2009 JFG (1) Ok, now I see where EQ17 comes in to the blog on 11/06/09. On 11/09/09 do you mean to say EQ16's partner is EQ17? Also, how about the symmetry group originally mentioned for EQ17 on 11/06/09: {e, σx, σxτz, τσxz}? That still doesn't make sense to me. Can you fix it up so I can double-check its conjugacy to R? (2) You're right, EQ7 is in {e,τxz}xS. (3) Good. (4) What's been giving you trouble with continuation? Let's talk on skype.

11/10/2009 DWS In my haste, I wrote down {e, σx, σxτz, τσxz} when I meant {e, σx, σzτz, σxzτz}. I used findsymmetries on the original equilibrium I found and it spit out:

 4
 1 1 1 1 0 0
 1 -1 -1 1 0 0
 1 1 1 -1 0 0.5
 1 -1 -1 -1 0 0.5

Knowing that this was probably conjugate to one of the isotropy groups listed in the EQB-TW JFM, I used:

 symmetryop -az 0.25 eq17.ff eq17max.ff
 findsymmetries eq17max.ff
 4
 1 1 1 1 0 0
 1 -1 -1 1 0 0
 1 1 1  -1 0 0
 1 -1 -1 -1 0 0

which indicates to me that the equilibrium is in the R isotropy group. I also can confirm a 3rd R-invariant equilibrium with dissipation 3.65963 and ||u|| = .325111. I also think that I have found an Rx-invariant periodic orbit with period 63.03 and D = 4.75123. It has converged down to L2Norm(G) = 2e-13, so it is close to converging to an official periodic orbit.

11/12/2009 DWS Found an Rz invariant equilibrium. It has an extremely high dissipation (5.54202) and Norm (0.427491). I'm pretty sure that none of the 4 solutions that I've found outside of S and {e,σxz} are important in the dynamics of PCF at Re=400. Maybe they contribute to the occasional bursting seen in this system. Nevertheless, now a solution in the Rz invariant space exists.

11/12/2009 PC Your batting's getting real good. Got one in each. They might be totally isolated, but you do not know that until you see their unstable manifolds - sometimes they shape the dynamics even though the equilibrium itself is very isolated. Or there might be short periodic orbits which are important, even though the equilibria are extreme.

But, JFG and DWS pray tell, why have we diverged away from the painfully composed 67 ways of killing group theoretical pain, and the logically chosen and named 5 isotropy group representatives, and are back to Waleffian S's and S3's and the like? I was showing the list of equilibria to Hof group here, and having two notations was not helpful to them…

11/17/2009 JFG Numerically we have not yet shifted to the logically chosen symmetry groups, out of shear laziness –changing O(100) GB of data on my hard drive is impractical, so I need a more surgical strike and then to live with pre-2010 data in one coord system and post-2010 in another. Maybe this would be a good project for Dustin, to replace all the solutions posted on the web with half-box shifted versions that are in the logical symmetry groups, and maybe revise channelflow utilities to either replace -s1 -s2 options with general group options, or at least revise them so they're in the right coordinate systems. It would be useful and a good way to ensure you understand PCF symmetries and conjugacies.

Predrag, an answer to your Dustin-blog question “why is ||u|| worth reporting?”: To me ||u|| is the crudest possible measure of a velocity field and is worthwhile in its complete lack of susceptibility to fooling us in ways we don't understand. It is a measure of “perturbation energy” (sqrt of energy of difference from laminar flow, give or take 1/2). ||u|| = 0 is laminar flow, ||u|| ≠ 0 is nonlaminar flow. Large ||u|| is far from laminar. In time-integration ||u|| ≈ 0 means the flow has decayed to laminar so you can stop. ||u|| » 1 (for non-dimensionalized flows) means the solution has blown up and that you probably have a numerical instability (time step too big). Other measures are not so simple. Dissipation is a also good measure, but it is nonlinear in u. Wall shear is also a good measure, but it depends only on the mean shear at the wall, so it tells you nothing about the interior. I believe is is still an open question whether or not there are other solutions with the same dissipation and shear as laminar. On a practical level, the concept of a norm is fundamental to many of our numerical algorithms, for measuring things like u-f^t(u) to determine whether or not we have a solution, ||du|| to see if a proposed Newton step is large or small, and these quantities need to be judged large or small relative to a “typical” norm ||u||.

11/17/2009 DWS A few questions and answers to Predrag that I don't want to litter my svn with.

1.) I am using Kile most of the time to edit my svn blog. Sometimes, when I'm lazy and don't want to wait for Kile to boot up, I simply use gedit for small edits.

2.) I am not entirely sure as to what all symmetries exist for pipe flow. It would seem to me that a continuous symmetry of rotation about the streamwise (I think you called it the x) axis would exist and the continuous symmetry for translations along the x-axis would also exist. I don't see there being any other symmetries than that. For duct flow, however, there would be the same discrete rotation symmetries as PCF, but only the one translational continuous symmetry in the x direction. If I am misunderstanding the symmetries inherent in a system, any analysis using the errant symmetries would be a waste.

Wedin & Kerswell JFM 2004 v 508 present four symmetry operations for pipe flow. The most important, the discrete rotation operation, is given by (forgive the random assignment of notation):

ℜ_m[u,v,w,p](s,Φ,z) = [u,v,w,p](s,Φ + 2π/m,z)

then the rotate-reflect:

T₁[u,v,w,p](s,Φ,z) = [-u,-v,w,p](-s,Φ + π,z)

then the reflect:

ℑ[u,v,w,p](s,Φ,z) = [u,-v,w,p](s,-Φ,z)

and finally the shift-reflect

T₂[u,v,w,p](s,Φ,z) = [u,-v,w,p](s,-Φ,z + π/α)

where α a wavenumber like in PCF. The position coordinates are given in cylindrical. Not sure about the velocity components yet.

11/21/2009 PC With all due respect to the established tradition, the registry of symmetries of Gibson, Halcrow, Cvitanović JFM 2009 v 638 seems more rational to me then the various shift-reflects, so I think we may be so bold as to use a similar (much simpler) list for pipes, as long as we clearly describe the conjugacies that map solutions in the literature to our classification. Our justification would be that we view pipes and planes as related problems.

I did some editing in the above, could not help myself: an equation or a solution has a symmetry (is invariant under given group action or operation). A group action is group action, not a 'symmetry'. I have continued this in spieker blog, not to type latex twice, and to be able to use our macros.

11/17/2009 JFG In Wedin & Kerswell JFM 2004 v 508, the axial direction is z, and u,v are azimuthal and radial velocity within the circular cross-sections. I think what you have listed above should be considered particular symmetries exhibited by solutions of pipe flow (like the S or R_xz group of plane Couette flow). We should start from the general symmetry group of pipe flow (like Γ in Gibson, Halcrow, Cvitanović JFM 2009 v 638) and consider particular solutions to have symmetries given by subgroups of that general group. The general symmetry group of pipe flow should be

[u,v,w,p](s,Φ,z) → [u,v,w,p](s, Φ + θ, z) continuous axial rotation
[u,v,w,p](s,Φ,z) → [u,-v,w,p](s, -Φ, z)   reflection about Φ=0 plane
[u,v,w,p](s,Φ,z) → [u,v,w,p](s, Φ, z + l_z) continuous translation in z

11/18/2009 DWS The channelflow revision number that was leading to unexpected continuations of EQ16 and (now) EQ19 was revision 308. It's been a while since I checked it out last.

11/19/2009 JFG Can you post some plots of the continuations and describe the problem in more detail? I am skypable today, too.