docs:utils:randomfield
Table of Contents
randomfield
Create a velocity field with
- random spectral coefficients that decay exponentially
- zero divergence
- Dirichlet boundary conditions at the walls
options
-Nx --Nx <int> # x gridpoints -Ny --Ny <int> # y gridpoints -Nz --Nz <int> # z gridpoints -a --alpha <real> default == 0 Lx = 2 pi/alpha -g --gamma <real> default == 0 Lz = 2 pi/gamma -lx --lx <real> Lx = 2 pi lx -lz --lz <real> Lz = 2 pi lz -sd --seed <int> default == 1 seed for random number generator -s --smoothnes <real> default == 0.4 smoothness of field, 0 < s < 1 -m --magnitude <real> default == 0.2 magnitude of field, 0 < m < 1 -mf --meanflow perturb the mean -s1 --s1-symmetry satisfy s1 symmetry -s2 --s2-symmetry satisfy s2 symmetry -s3 --s3-symmetry satisfy s3 symmetry <fieldname> (trailing arg 1) output file
mathematics
The field takes the form
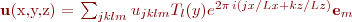
where the spectral coefficients are assigned according to
![LaTeX
u_{jklm} = (\text{random # in }[-1, 1]) * \text{(1-smoothness)}^{|l| + |j| + |k|}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgb8d675da38d5323e77f925cc94d85460.png)
with corrections to meet boundary and divergence conditions and rescaling so that L2Norm(u) = magnitude.
The form of spectral decay chosen is crude, but normally what is needed in a random field is that
it meets the BCs and zero-div, is controllably smooth, and excites modes with all symmetries. It would probably be better to work the length scales Lx,Ly,Lz into the exponent of (1-smoothness), so that the variations in the random field are roughly spatially isotropic.
docs/utils/randomfield.txt · Last modified: 2010/02/02 07:55 (external edit)
