Create a velocity field with

• random spectral coefficients that decay exponentially
• zero divergence
• Dirichlet boundary conditions at the walls

  -Nx       --Nx             <int>                     # x gridpoints
  -Ny       --Ny             <int>                     # y gridpoints
  -Nz       --Nz             <int>                     # z gridpoints
  -a        --alpha          <real>   default == 0     Lx = 2 pi/alpha
  -g        --gamma          <real>   default == 0     Lz = 2 pi/gamma
  -lx       --lx             <real>                    Lx = 2 pi lx
  -lz       --lz             <real>                    Lz = 2 pi lz
  -sd       --seed           <int>    default == 1     seed for random number generator
  -s        --smoothnes      <real>   default == 0.4   smoothness of field, 0 < s < 1
  -m        --magnitude      <real>   default == 0.2   magnitude  of field, 0 < m < 1
  -mf       --meanflow                                 perturb the mean
  -s1       --s1-symmetry                              satisfy s1 symmetry
  -s2       --s2-symmetry                              satisfy s2 symmetry
  -s3       --s3-symmetry                              satisfy s3 symmetry
  <fieldname>  (trailing arg 1)                        output file

The field takes the form

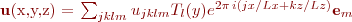
where the spectral coefficients are assigned according to

with corrections to meet boundary and divergence conditions and rescaling so that L2Norm(u) = magnitude.

The form of spectral decay chosen is crude, but normally what is needed in a random field is that it meets the BCs and zero-div, is controllably smooth, and excites modes with all symmetries. It would probably be better to work the length scales Lx,Ly,Lz into the exponent of (1-smoothness), so that the variations in the random field are roughly spatially isotropic.