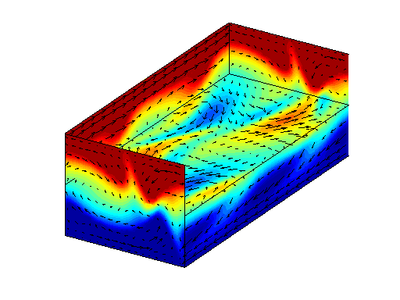
Here are the first twelve (12) eigenvectors of the UB equilibrium: — Dustin Spieker 2009-03-25
e_1 
Re e_2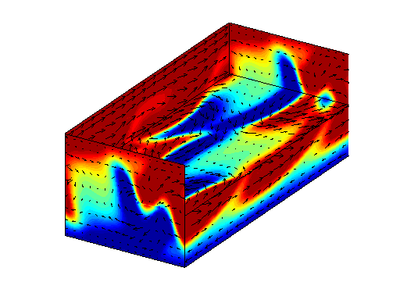 
Im e_2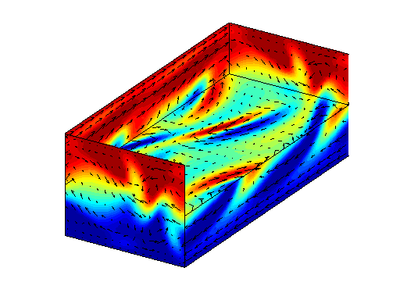 
Re e_4 
Im e_4 
Re e_6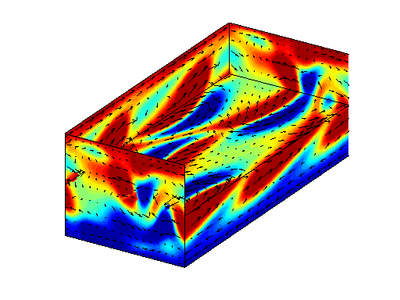 
Im e_6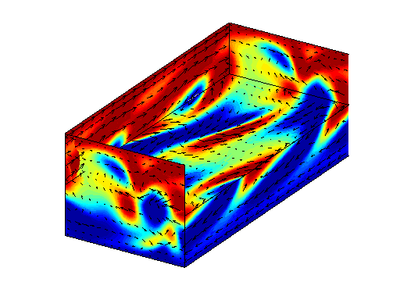 
e_8 
[2 marginal eigenvalues - do they have nontrivial eigenvectors?]
Re e_11 
Im e_11 
e_13 
Re e_14 
Thanks. They are the full space eigenvalues, not restricted to S-invariant subspace, right? I have labeled them correctly? (Re e_11,Im e_11) is the least contracting stable eigenvalue pair? 400 x 300 pixels is good, but in the next version, can you crop them tightly, remove the white acreage around them?
Compare with JohnG's blog (he has about 20 of them, so there might be a better version - I'm not strong enough to find it). — Predrag Cvitanovic 2009-03-27 12:23
A couple suggestions: It might make be better to plot these fields with the laminar flow removed.
They're eigenfunctions of EQ2, so if they're superimposed on anything, it should be that. But best on their own, I think. Also, the scale of these fields is arbitrary. You can play around with the scale parameter of the matlab plotbox function to get less saturation of red and blue.
I vote for not subtracting the laminar flow. Adding a constant to u(x,t) does not change the matrix of state-space velocity gradients A, or its eigenvalues, eigenvectors. Do play with the scale parameter. I'm curious: what do the the eigenvectors of the two marginal eigenvalues look like? They should point along the two continuous translations, streamwise and spanwise. Perhaps obvious…
I found a better zoom to make the plots better in 400×300. I'll look into the scaling now. — Dustin Spieker 2009-03-29 09:21
