Table of Contents
The plane pendulum
Mathematical models
In class we derived four different mathematical models of the plane pendulum, listed here in order of decreasing mathematical complexity.
Nonlinear damped pendulum. This is the most physically realistic model. It includes a linear model of air resistance the 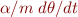 term and is accurate for large displacement angles
term and is accurate for large displacement angles  .
.
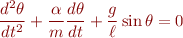
Nonlinear undamped pendulum. This model neglects air resistance. It is derived from the previous model by setting the air resistance constant  to zero.
to zero.
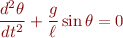
Linear damped pendulum. This is valid only for small oscillations. You can derive it from the nonlinear damped pendulum model by substituting the small angle approximation  for small
for small  .
.
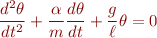
Linear undamped pendulum. The simplest pendulum model. It neglects air resistance and employs the small-angle approximation.
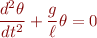
In each of these, the variables are
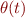 : the unknown function that describes the angle of the pendulum away from vertical as a function of time.
: the unknown function that describes the angle of the pendulum away from vertical as a function of time. : the mass of the pendulum bob.
: the mass of the pendulum bob. : the length of the pendulum string
: the length of the pendulum string : the acceleration of gravity
: the acceleration of gravity : an air resistance constant
: an air resistance constant
In class we showed that the linear undamped pendulum has a solution of the form  where
where 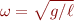 and
and  is an arbitrary initial angular displacement. (Note that
is an arbitrary initial angular displacement. (Note that  must be small for the small-angle approximation to be valid!)
must be small for the small-angle approximation to be valid!)
Changing a second-order ODE into a system of first-order ODEs
A 2nd-order ordinary differential equation in the scalar variable 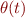 can be transformed into a 1st order equation in the vector variable
can be transformed into a 1st order equation in the vector variable 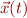 , using the substitution
, using the substitution
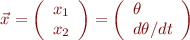
For example, to transform the linear undamped pendulum equation 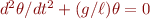 ,
let
,
let  and
and 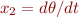 . Differentiate those two equations to get
. Differentiate those two equations to get
 and
and  . Now note that, according to the linear undamped pendulum equation,
. Now note that, according to the linear undamped pendulum equation, 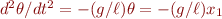 . Putting all this together, we can write
. Putting all this together, we can write

This equation is now of the form 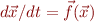 , so it can be solved numerically with Matlab's
, so it can be solved numerically with Matlab's ode45 function.
