Table of Contents
Math 445: fprintf, for loops, functions
fprintf: formatted printing
fprintf is Matlab's formatted print function. It's used for printing variables to the screen (or files) in a format that you specify. The basic syntax is
fprintf('format-string', variable, variable, variable, ...)
but it is really best illustrated by example.
>> w = 'perambulate'; >> n = length(w); >> fprintf('The word %s has %d letters.\n', w, n) The word perambulate has 11 letters.
The format string contains two slots %s and %w. The percent sign is a special marker that signals a slot, and the character following it specifies the type of variable that goes in the slot, %s for string and %d for decimal. The values of the variables  and
and  are placed in those slots when the fprintf function is executed. The
are placed in those slots when the fprintf function is executed. The \n is a special control character for “new line.”
The most important slot types are
%ddecimal (integer), e.g. 5%ffloating-point, e.g. 2.75%efloating-point in scientific (exponential) notation, e.g. 2.75e+00 for 2.75%sstring (a sequence of characters), e.g.'banana'.%ccharacter, e.g.'q'
The decimal and floating-point slots can be specialized to print numbers in particular ways, for example,
>> fprintf('The value of pi is %8.3f\n', pi) The value of pi is 3.142
This prints  with 3 digits after the decimal in a fixed-width field of 8 characters.
with 3 digits after the decimal in a fixed-width field of 8 characters.
You can put as many slots in a format string as you like. Just provide as many variables as slots, and make sure the types of the slots match the variables.
for loops: repeating sequences of commands
for loops are used to repeat a sequence of commands a specified number of times. A for loop has an index variable (often  or
or  ) whose value changes over every iteration of the loop. For example, this Matlab for loop
) whose value changes over every iteration of the loop. For example, this Matlab for loop
for n=1:4 fprintf('The value of n is %d.\n',n); end
produces the output
The value of n is 1. The value of n is 2. The value of n is 3. The value of n is 4.
Note how the body of the loop (the fprintf) statement is executed four times, once for each value of  from 1 to 4.
from 1 to 4.
functions
The Matlab function command lets you define your own functions. For example, putting
the following code in a file named quadratic.m
- quadratic.m
function y = quadratic(x) y = x^2 + 3*x -7; end
defines a function named quadratic that computes the polynomial 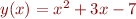 . The filename must match the name of the function. If the
. The filename must match the name of the function. If the quadratic.m function is in Matlab's current working directory, you'll be able to execute the function just like a regular Matlab built-in function, for example
>> quadratic(0)
ans =
-7
>> quadratic(1)
ans =
-3
>> quadratic(12.74)
ans =
193.5276
example functions
sum the components of a vector
This mysum function computes the sum of the components in the input vector  . There are a
number of extraneous print statements which show how the calculation works, step-by-step.
. There are a
number of extraneous print statements which show how the calculation works, step-by-step.
- mysum.m
function s = mysum(x); % compute the sum of the components of vector x s = 0; % variable to hold partial sum n = length(x); % get length of vector x fprintf('Will need to do %d additions.\n\n', n); for i=1:n fprintf('The current partial sum is s = %f.\n\n', s); pause fprintf('Add %f.\n', x(i)); s = s + x(i); end fprintf('The total sum is s = %f.\n', s); pause end
You can execute this function with on the input vector [4 2 9 1]] like this
>> mysum([4 2 9 1])
Will need to do 4 additions.
The current partial sum is s = 0.000000.
Add 4.000000.
The current partial sum is s = 4.000000.
Add 2.000000.
The current partial sum is s = 6.000000.
Add 9.000000.
The current partial sum is s = 15.000000.
Add 1.000000.
The total sum is s = 16.000000.
ans =
16
>>
The function is a lot easier to read if you take out the print statements
compute the factorial
This function computes 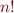 , the factorial of
, the factorial of  , according to the formula
, according to the formula

- myfactorial.m
function p = myfactorial(n); % compute factorial of n = 1 * 2 * ... (n-2)*(n-1)*n p = 1; % variable to store partial products % each step through the loop does one more multiplication % in the sequence of products 1, 1*2, 1*2*3, etc. for i=1:n p = p * i; end end
