Lab 7: Nonlinear equations and Newton's method
In this lab you will
- write your first numerical algorithm
- learn the most widely-used algorithm for solving nonlinear equations
- solve a practical, real-world problem involving a nonlinear equation
- learn about anonymous functions
- gain more experience in programming with
forloops andifstatements
Problem 1: Write a function x = newtonsearch(f, xguess) that finds the solution
x of the equation f(x) = 0 for an input function f and an initial guess
xguess using the Newton search algorithm.
Your Newton search algorithm should
1. Use a for loop to perform the Newton-search iteration 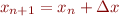 . Take up to ten Newton-search iterations.
. Take up to ten Newton-search iterations.
2. Use an if statement inside the for loop to test if either  or
or  for some specified tolerance
for some specified tolerance  .
.
3. If either of those conditions is true, use a break statement to terminate the iteration and return from the function. For our purposes  is a decent choice.
is a decent choice.
Problem 2: Test your Newton-search algorithm by solving the following problems. Check your
answers by plugging the answer x back into f and verifying that f(x) is approximately
zero.
(a) Find an  for which
for which 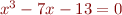 .
.
(b) Find the cube root of 72 by devising and solving an equation of the form  whose
solution is
whose
solution is ![Math $x = \sqrt[3]{72}$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img67106bddfe7fa265bc03b4793849ac12.png) . Is there a simpler way to calculate
. Is there a simpler way to calculate ![Math $\sqrt[3]{72}$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img06bf37d6e5fc6850d67122faedaa4334.png) in Matlab?
Do that, and compare your answers.
in Matlab?
Do that, and compare your answers.
(c) Find an  for which
for which  .
.
Hint: find good initial guesses for the Newton search by plotting each function and roughly
estimating an  position at which
position at which 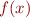 is zero.
is zero.
Problem 3: Use your Newton-search algorithm to solve the following problem. Utility
companies must avoid freezing water mains in cold weather. If we assume uniform soil
conditions, the temperature 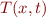 at distance
at distance  below the surface and time
below the surface and time  after the beginning of a cold spell is given approximately by
after the beginning of a cold spell is given approximately by
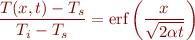
where
 is the constant surface temperature during the cold spell,
is the constant surface temperature during the cold spell, is the initial soil temperature before the cold spell started,
is the initial soil temperature before the cold spell started, is the thermal conductivity of the soil, and
is the thermal conductivity of the soil, and  is the error function, computed by the built-in Matlab function erf.
is the error function, computed by the built-in Matlab function erf.
If  is in meters and
is in meters and  is in seconds, the thermal conductivity of soil is
is in seconds, the thermal conductivity of soil is
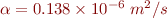 .
Let
.
Let  and
and  , and recall that water freezes at
, and recall that water freezes at  .
Use your Newton-search algorithm to determine how deep a water main must be
buried so that it will not freeze until at least 60 days' exposure to these
conditions.
.
Use your Newton-search algorithm to determine how deep a water main must be
buried so that it will not freeze until at least 60 days' exposure to these
conditions.
