Math 445 lab 11: home run
It is easy to determine the trajectory of a projectile subject to gravity if you neglect air resistance. It is much more difficult to solve if you include air resistance, especially if the flow becomes turbulent and the resistive force is nonlinear. We can solve the nonlinear case only numerically.
For this lab, you will determine the minimum speed and optimal angle at which to hit a baseball in order to score a home run, both at sea level (Fenway) and at high altitude (Denver). Assume that
- the ball is hit 1 meter above home plate at speed
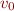 and angle
and angle  .
. - the outfield fence is 120 meters (394 feet) from home plate and 3 meters high (about 10 feet).
Problem 1: Write a Matlab function that computes and plots the trajectory of the baseball and determines whether the ball clears the outfield fence. The function inputs should be 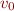 and
and  , and the output should be the height of the ball when it reaches the fence.
, and the output should be the height of the ball when it reaches the fence.
Use the following equations of motion, developed during class




The constant  is the acceleration due to gravity. The constant
is the acceleration due to gravity. The constant  in the air resistance term depends on physical characteristics of the projectile and the air. The following code will calculate
in the air resistance term depends on physical characteristics of the projectile and the air. The following code will calculate  for a standard baseball, given either value of
for a standard baseball, given either value of 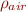 .
.
rho_air = 1.196; % kg/m^3, density of dry air, 21 C, sea level (Fenway) rho_air = 0.986; % kg/m^3, density of dry air, 21 C, 1 mile high (Denver) C_D = 0.3; % drag coefficient for baseball (rough sphere) g = 9.81; % acceleration due to gravity in m/s^2 r = 0.0375; % radius of baseball in m (3.75 cm) A = pi*r^2; % cross-sectional area of baseball in m^2 m = 0.145; % mass of baseball in kg (145 gm alpha = rho_air*C_D*A/2; % coefficient of nonlinear |v|^2 term, in mks units
Problem 2: Determine the minimum initial ball speed and optimal angle that result in a home run, at sea level, and in Denver. You'll have to start with a guesses for 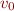 and
and  and tweak them by stages. For a starting point, recall that a good fastball clocks at 90 mph or roughly 40 m/s, and that the optimal angle is
and tweak them by stages. For a starting point, recall that a good fastball clocks at 90 mph or roughly 40 m/s, and that the optimal angle is  when there is no air resistance.
when there is no air resistance.
Note that Matlab's ode45 function will return the x,y positions of the trajectory points at discrete time intervals, and it's unlikely that any of these will line up exactly with the outfield fence. However you can use interpolation to get the ball height y at exactly at the fence, as follows. If you set up your Matlab code so that  is x(:,1) and
is x(:,1) and  is x(:,2), the following code will determine the height
is x(:,2), the following code will determine the height  of the ball at the position of the fence,
of the ball at the position of the fence,  .
.
yfence = interp1(x(:,1), x(:,2), 120);
Problem 3: Make a plot that shows the  trajectory of the homerun hit with the minimal speed and optimal angle for sea level conditions, which you determined in problem 2. Now add another curve that shows what the path of that ball would be if there were no air resistance. Use a solid line for the curve with air resistance, and a dashed line for the curve without.
trajectory of the homerun hit with the minimal speed and optimal angle for sea level conditions, which you determined in problem 2. Now add another curve that shows what the path of that ball would be if there were no air resistance. Use a solid line for the curve with air resistance, and a dashed line for the curve without.
Problem 4: Do the same as problem 3 for the home run in Denver.
Problem 5: What are your answers for the minimal speed and optimal angle in the more familiar units of miles per hour and degrees, for both Boston and Denver?
