Table of Contents
Math 445 lectures 18, 19: time-stepping
How do you figure out the path 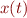 of a object whose velocity
of a object whose velocity 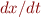 is a given function of its position
is a given function of its position  ? I.e., given that
? I.e., given that
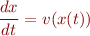
for some known function 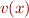 , along with an initial position
, along with an initial position 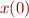 , how do you solve for the path
, how do you solve for the path 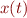 ? (Note that here
? (Note that here  and
and  should be considered vector-valued quantities. I'm leaving out the arrows on top to reduce clutter.)
should be considered vector-valued quantities. I'm leaving out the arrows on top to reduce clutter.)
The above equation is an ordinary differential equation. MATH 527 Differential Equations is all about finding solutions to such equations in closed form. Here we will use numerical solution methods to find approximate numerical solutions.
To make things concrete, let's solve the following problem. Given the 2D inviscid flow around a cylinder from the last lecture, what would be the path of a small particle starting at position  , shown below as a red circle?
, shown below as a red circle?
Here's the code for plotting the 2D inviscid cylinder flow. The line x = [-3.8, 0.6]; plot(x(1), x(2), 'ro'); plots the dot. The problem now is to compute and plot the particle as it's advected along by the fluid velocity field 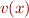 , where
, where
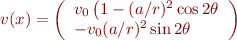
and where 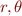 are the polar coordinates of the vector position
are the polar coordinates of the vector position 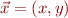 .
.
Problem 1
Write Matlab code that plots the motion of the particle, in discrete steps, using the forward-Euler timestepping formula
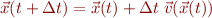
This equation says, essential that the distance a particle moves in a small time interval  is given by the product of
is given by the product of  and the velocity
and the velocity 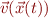 .
.
Here's some Matlab code that implements the forward Euler timestepping with a simple for loop.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Simulate a particle moving through the inviscid cylinder flow % using forward Euler time-stepping % % x(t + dt) = x(t) + dt*v(x(t)); % % Integrate from t=0 to t=9 in small steps of length dt (say dt=0.1) % That is, find the path x(t) for 0 <= t <= 9. T = 9; dt = 0.4; Nsteps = round(T/dt); x = [-2.8; 0.6]; % initial position of particle hold on; for n=1:Nsteps; plot(x(1), x(2), 'ro') x = x + dt*v(x); % update position using forward euler pause end
Note that the above code calls a function v(x), which is defined in the Matlab function file v.m
- v.m
function dxdt = v(x) % return velocity vector v(x) for cylinder flow at position x V0 = 1; a = 1; r = sqrt(x(1)^2 + x(2)^2); theta = atan2(x(2),x(1)); dxdt = [V0*(1 - a^2/r^2 * cos(2*theta)); -V0*a^2/r^2 * sin(2*theta)]; end
Note that the trajectory computed here is not very accurate. The particle shouldexit the box at the same  value it had when it entered. The problem is we chose quite a large time step
value it had when it entered. The problem is we chose quite a large time step  , and forward-Euler is only 1st-order accurate (error scales as
, and forward-Euler is only 1st-order accurate (error scales as  ). In the next problem, we'll reduce the time step to
). In the next problem, we'll reduce the time step to  and get a more accurate solution –though still not as good as the 4th-order accurate
and get a more accurate solution –though still not as good as the 4th-order accurate ode45 function.
Problem 2
Write Matlab code that plots the path of the particle as a red curved line. To do this we need to save the sequence of  values in a matrix, and then plot the rows of that matrix as a line.
values in a matrix, and then plot the rows of that matrix as a line.
T = 10; % integrate from t=0 to T=10, i.e 0 <= t <= 10 dt = 0.01; % Nsteps = round(T/dt); X = zeros(2,Nsteps); % stores sequences of x(t) values as cols in a matrix X(:,1) = [-2.8; 0.1]; % initial position of particle for n=1:Nsteps X(:,n+1) = X(:,n) + dt*v(X(:,n)); % forward euler time stepping end plot(X(1,:), X(2,:), 'r-'); axis equal axis tight xlim([-3,3]) ylim([-2,2])
Problem 3
Write Matlab code that plots the path of the particle as a red curved line, using Matlab's ode45 function to do the time-integration.
% use Matlab's ode45 function to do the time integration of % dx/dt = v(t, x) T = 10; % integrate from t=0 to T=10 x0 = [-2.8; 0.6]; % initial position of particle [t, x] = ode45(@v, [0 T], x0); % computes x(t) at given values of t plot(x(:,1), x(:,2), 'r-'); axis equal axis tight xlim([-3,3]) ylim([-2,2])
Matlab's ode45 function requires an ODE of the form 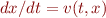 , so we have to add a
, so we have to add a t argument to our v function
- v.m
function dxdt = v(t, x); % compute 2D inviscid cylinder velocity as function of x % input: vector x has x(1) = x coord, x(2) = y coord V0 = 1; % scale of velocity a = 1; % radius of circle % compute polar coordinates r = sqrt(x(1)^2 + x(2)^2); theta = atan2(x(2), x(1)); dxdt = [V0*(1 - (a/r)^2 * cos(2*theta)) ; -V0*(a/r)^2 * sin(2*theta)]; end
This produces a plot very like the one for Problem 3.
Problem 4
Draw a number of particle paths starting with a number of  values and
values and  .
.
% use Matlab's ode45 function to do the time integration of % dx/dt = v(t, x) T = 10; % integrate from t=0 to T=10 for y = -2:0.4:2 % loop over different y values x0 = [-2.8; y]; % set initial position of particle [t, x] = ode45(@v, [0 T], x0); % compute x(t) over range 0 <= t <= T plot(x(:,1), x(:,2), 'r-'); % plot the path end




