gibson:teaching:fall-2016:math753:finalexam
Math 753/853 final exam topics
Wed, Dec 14, 2016 10:30am-12:30pm Kingsbury N343
Floating point numbers
- binary representation
- how #s of bits in mantissa and exponent lead to # digits in same
- floating point arithmetic: expected accuracy of arithmetic operations
- what is machine epsilon?
Solving 1d nonlinear equations
- bisection: the algorithm, the required conditions, the convergence rate
- Newton: the algorithm, the required conditions, the convergence rate
- when to use bisection, when to use Newton
Gaussian elimination / LU decomposition
- the LU algorithm: what are the formulae for computing the multipliers
 of
of  ?
? - be able to compute the LU decomp of a small matrix by hand
- backsubstitution, forward substitution
- using LU to solve

- pivoting –what is it, why is it a practical necessity?
- what form does the LU decompostion take with pivoting? How do you use this form to solve
 ?
?
QR decomposition
- what is a QR decomposition?
- what algorithm do you know for computing the QR decomposition?
- what are the formulae for the elements
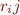 of
of 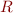 and the column vectors
and the column vectors 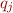 of
of  ?
? - what is an orthogonal matrix?
- how to use QR decomp to solve a square
 problem
problem - how to use QR decomp to find a least-squares solution to an oblong
 problem (
problem ( matrix
matrix 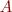 , with
, with  )
)
Polynomials
- Horner's method: be able to rearrange a polynomial into Horner's form, and understand why you'd do that
- Lagrange interpolating polynomial: be able to write down the Lagrange interpolating polynomial passing through a set of data points
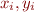 , and understand why the formula works
, and understand why the formula works - Newton divided differences: know how to use this technique to find the interpolating polynomial through a set of data points
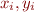
- Chebyshev points: what are they, what are they good for, why do we need them?
Least-squares models
- Understand how to set up least-squares
 problems to find the best fit for functions of the following forms to
problems to find the best fit for functions of the following forms to  pairs of datapoints
pairs of datapoints 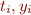
- an
 th order polynomial
th order polynomial - an exponential
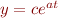
- a power law

- a curve of the form
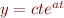
Finite differencing and quadrature
- be able to approximate the first & second derivatives of a function
 from the values
from the values 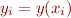 where the
where the  are evenly spaced gridpoints
are evenly spaced gridpoints 
- provide error estimates of those approximate derivatives
- be able to approximate the integral
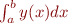 of the function
of the function  from evenly space gridpoint values
from evenly space gridpoint values 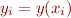 , using the Trapeziod Rule and Simpson's rule
, using the Trapeziod Rule and Simpson's rule - provide error estimates for those approximate integrals
Ordinary differential equations
- what is an initial value problem?
- why do we need to solve initial value problems numerically?
- what are the timestepping formulae for
- Forward Euler
- Midpoint Method (a.k.a. 2nd order Runge-Kutta)
- 4th-order Runge-Kutta
- Backwards Euler
- Adams-Moulton
- what are the global error estimates of the above timestepping formulae?
- what is a global error estimate versus a local error estimate, and how are the two related?
- what's the difference between an explicit method and an implicit method?
- what's a stiff differential equation? what kind of method do you use for a stiff equation?
- how do you convert an
 th order differential equation in one variable to a system of first order differential equations in
th order differential equation in one variable to a system of first order differential equations in  variables?
variables?
gibson/teaching/fall-2016/math753/finalexam.txt · Last modified: 2016/12/12 19:00 by gibson
