IAM 961 HW5
Problem 1: Implement Rayleigh quotient iteration and demonstrate its convergence, as follows. Develop your code with a small matrix (maybe 5 x 5) and do the final demonstration with a larger matrix (maybe 100 x 100).
1. Construct a random symmetric M x M matrix A with random but known eigenvalues and eigenvectors. Hint: construct A from a random orthogonal matrix V and a known random diagonal matrix D. (4 lines of code).
2. Select a eigenvalue of A and the corresponding eigenvector (an element of D and a column of V). Verify that these are in fact an eigenvalue, eigenvector pair. (3 lines of code).
3. To get an initial guess for the Rayleigh quotient iteration, perturb the eigenvector by 10% or so and evaluate the Rayleigh quotient using the perturbed eigenvector. (5 lines of code).
4. Now do the Rayleigh quotient iteration, stopping when  . Plot the errors in the eigenvalue and eigenvector as a function of the iteration number. The Rayleigh quotient iteration code takes about 3 lines of code, the plotting more. Don't forget to label your axes!
. Plot the errors in the eigenvalue and eigenvector as a function of the iteration number. The Rayleigh quotient iteration code takes about 3 lines of code, the plotting more. Don't forget to label your axes!
Answer these questions:
Are you amazed, or what?
Can you confirm that the errors scale as stated on page 208 of Trefethen and Bau?
Note: the suggested line counts above are not requirements. They're meant as guidelines to let you know how roughly how much code each line should require. If you're writing more, you're working too hard.
Problem 2: Implement GMRES and investigate its convergence as a function of the matrix condition number, as follows. Given a value of  and
and  , write code that will
, write code that will
1. Construct a random M x M matrix A with condition number  and exponentially graded singular values,
and exponentially graded singular values, 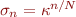 .
.
2. Let  be a random M vector with normally-distributed components. Let
be a random M vector with normally-distributed components. Let 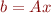 .
.
3. Do the GMRES iteration and plot the normalized residual 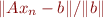 and the normalized
and the normalized  error
error 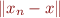 as a function of the iteration number
as a function of the iteration number  . Plot the residual with circles and the error with dots, put them on the same plot, and use a logarithmic axis for the errors: e.g.
. Plot the residual with circles and the error with dots, put them on the same plot, and use a logarithmic axis for the errors: e.g. semilogy(n,error,'b.',n,residual,'ro').
For testing and developing your code, set  to a small number like 10 and
to a small number like 10 and  to
to 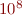 . Your GMRES code should go all the way to
. Your GMRES code should go all the way to 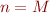 iterations. Your code should have a for-loop to handle iterations
iterations. Your code should have a for-loop to handle iterations  to
to 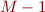 followed by some special-case code to handle the last
followed by some special-case code to handle the last 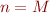 th iterate –the last iteration works a little differently.
th iterate –the last iteration works a little differently.
Once your code is working (the residual is 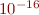 at the last iterate), set
at the last iterate), set  to a moderately small number like 30 and produce four residual-and-error plots, for
to a moderately small number like 30 and produce four residual-and-error plots, for 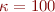 ,
, 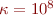 ,
, 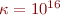 , and
, and 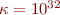 .
.
Discuss your results. Is anything surprising? What can you explain about the behavior of the plots, given what you know about GMRES and  problems in general?
problems in general?
