fprintf is Matlab's formatted print function. It's used for printing variables to the screen (or files) in a format that you specify. The basic syntax is

fprintf('format-string', variable, variable, variable, ...)

but it is really best illustrated by example.

>> w = 'perambulate';
>> n = length(w);
>> fprintf('The word %s has %d letters.\n', w, n)
The word perambulate has 11 letters.

The format string contains two slots %s and %w. The percent sign is a special marker that signals a slot, and the character following it specifies the type of variable that goes in the slot, %s for string and %d for decimal. The values of the variables and are placed in those slots when the fprintf function is executed. The \n is a special control character for “new line.”

The most important slot types are

• %d decimal (integer), e.g. 5
• %f floating-point, e.g. 2.75
• %e floating-point in scientific (exponential) notation, e.g. 2.75e+00 for 2.75
• %s string (a sequence of characters), e.g. 'banana'.
• %c character, e.g. 'q'

The decimal and floating-point slots can be specialized to print numbers in particular ways, for example,

>> fprintf('The value of pi is %8.3f\n', pi)
The value of pi is    3.142

This prints with 3 digits after the decimal in a fixed-width field of 8 characters.

You can put as many slots in a format string as you like. Just provide as many variables as slots, and make sure the types of the slots match the variables.

for loops are used to repeat a sequence of commands a specified number of times. A for loop has an index variable (often or ) whose value changes over every iteration of the loop. For example, this Matlab for loop

for n=1:4
   fprintf('The value of n is %d.\n',n);
end

produces the output

The value of n is 1.
The value of n is 2.
The value of n is 3.
The value of n is 4.

Note how the body of the loop (the fprintf) statement is executed four times, once for each value of from 1 to 4.

The Matlab function command lets you define your own functions. For example, putting the following code in a file named quadratic.m

quadratic.m

function y = quadratic(x)
  y = x^2 + 3*x -7;
end

defines a function named quadratic that computes the polynomial 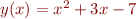. The filename must match the name of the function. If the quadratic.m function is in Matlab's current working directory, you'll be able to execute the function just like a regular Matlab built-in function, for example

>> quadratic(0)
ans =
    -7

>> quadratic(1)
ans =
    -3
 
>> quadratic(12.74)
ans =
  193.5276

This mysum function computes the sum of the components in the input vector . There are a number of extraneous print statements which show how the calculation works, step-by-step.

mysum.m

function s = mysum(x);
% compute the sum of the components of vector x
 
  s = 0;           % variable to hold partial sum
  n = length(x);   % get length of vector x
 
  fprintf('Will need to do %d additions.\n\n', n);
 
  for i=1:n
    fprintf('The current partial sum is s = %f.\n\n', s);
    pause
    fprintf('Add %f.\n', x(i));
    s = s + x(i);
  end
 
  fprintf('The total sum is s = %f.\n', s);
  pause
end

You can execute this function with on the input vector [4 2 9 1]] like this

>> mysum([4 2 9 1])
Will need to do 4 additions.

The current partial sum is s = 0.000000.

Add 4.000000.
The current partial sum is s = 4.000000.

Add 2.000000.
The current partial sum is s = 6.000000.

Add 9.000000.
The current partial sum is s = 15.000000.

Add 1.000000.
The total sum is s = 16.000000.
ans =
    16
>> 

The function is a lot easier to read if you take out the print statements

mysum.m

function s = mysum(x);
% compute the sum of the components of vector x
 
  s = 0;           % variable to hold partial sum
  n = length(x);   % get length of vector x
 
  for i=1:n        % for each number i from 1 to n
    s = s + x(i);  %    add x(i) to the partial sum
  end
 
end

This function computes 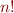, the factorial of , according to the formula

myfactorial.m

function p = myfactorial(n);
% compute factorial of n = 1 * 2 * ... (n-2)*(n-1)*n
 
  p = 1;   % variable to store partial products
 
  % each step through the loop does one more multiplication
  % in the sequence of products 1, 1*2, 1*2*3, etc.
  for i=1:n
    p = p * i;
  end
 
end