IAM 950 HW2
For this HW, you have a choice: compute periodic orbits of the Lorenz or the Rössler system. I demoed Lorenz in class, but you will learn a lot doing the numerics for yourself. Or you can do Rössler –it's simpler in a number of ways, but it would be more of an adventure into the unknown.
Choice 1: The Lorenz system
Compute all periodic orbits of the Lorenz ODE up to period 4 and produce a plot for each, like these.
Use the classic parameter values  . Use whatever software system you like (Matlab, Julia, Mathematica, C, Fortran, whatever). Compute the orbits with these steps.
. Use whatever software system you like (Matlab, Julia, Mathematica, C, Fortran, whatever). Compute the orbits with these steps.
Step 1: Plot the three unstable equilibria with dots. Compute and plot the stable manifold of the origin and a portion its unstable manifold as shown (magenta for stable manifold, blue and green for stable).
Step 2: Plot the pseudo-Poincare section given by the curve 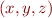
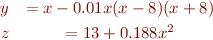
for  . This 1d curve lies pretty nearly on the attracting set. (I got it by guessing the right form and setting the constants by trial and error). Parameterize this curve numerically by
. This 1d curve lies pretty nearly on the attracting set. (I got it by guessing the right form and setting the constants by trial and error). Parameterize this curve numerically by  so that
so that  is
is  at the end points and zero at the center (simplest strategy: let
at the end points and zero at the center (simplest strategy: let 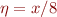 ).
).
Step 3: Let 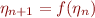 be the return map of
be the return map of  onto itself (hand-wavey, because trajectories starting on the
onto itself (hand-wavey, because trajectories starting on the  curve don't actually come back exactly to
curve don't actually come back exactly to  ). Create a table of
data of
). Create a table of
data of 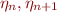 pairs by numerical integration of
pairs by numerical integration of 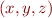 points starting on the
points starting on the  curve. Make a plot of
curve. Make a plot of 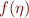 using this numerical data.
using this numerical data.
Step 4: Fit a function 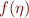 to the the numerical data from above. A piecewise polynomial with three or four terms should do. Plot this
to the the numerical data from above. A piecewise polynomial with three or four terms should do. Plot this 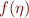 on top of your numerical values.
on top of your numerical values.
Step 5: Plot 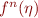 versus
versus  along with the diagonal to get an estimate of the
along with the diagonal to get an estimate of the  value of the period-n orbit. Then use the corresponding
value of the period-n orbit. Then use the corresponding  values as an initial guess for a periodic orbit.
values as an initial guess for a periodic orbit.
Step 6: Compute the periodic orbit, either approximately by adjusting  until the trajectory very nearly lands back on its starting point, or better, by setting up a function
until the trajectory very nearly lands back on its starting point, or better, by setting up a function 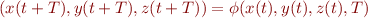 which maps
which maps  forward time
forward time  under the Lorenz dynamics, using numerical integration, and then applying a nonlinear numerical solution method to find a zero of the function
under the Lorenz dynamics, using numerical integration, and then applying a nonlinear numerical solution method to find a zero of the function 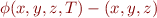 .
.
Choice 2: The Rössler system
Compute the first four or five periodic orbits of the Rössler system

with 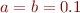 and
and  . A long trajectory of the Rössler system looks like this
. A long trajectory of the Rössler system looks like this
Step 1: Find the equilibria and the eigenvalues of the equilibrium near the origin. What is the period of the revolution about the equilibrium and the growth factor per revolution?
Step 2: Let the  plane define a Poincare section. Trajectories crossing this plane with
plane define a Poincare section. Trajectories crossing this plane with  increasing will have
increasing will have  very nearly zero, so the value of
very nearly zero, so the value of  at
at  serves as a good coordinate for a 1d return map. The above picture has a black line drawn from
serves as a good coordinate for a 1d return map. The above picture has a black line drawn from 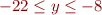 with
with  . Figure out a good parameterization to
. Figure out a good parameterization to ![Math $\eta = [0,1]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img0095ac2effb28a0bd01620f3f523d87f.png) of a subset of this line and construct a 1d return map by integrating trajectories from points on it.
of a subset of this line and construct a 1d return map by integrating trajectories from points on it.
Step 3: Approximate the numerical return map from step 2 with an analytic function, then use the fixed points of higher-order iterates of the return map to get initial guesses for periodic orbits.
Step 4: Find periodic orbits numerically by solving a nonlinear equation as described in step 6 for Lorenz.



