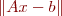IAM 961: Numerical Linear Algebra
Instructor: John Gibson, john.gibson@unh.edu
Office hours: Tue 2-3pm, Thu 12-1pm, Kingsbury N309E, or after class
Numerical linear algebra is the science of solving systems of linear equations 
and the eigenvalue problem
on a digital computer –problems are at the root of the vast bulk of scientific computation.
Compared to classical linear algebra, the finite precision and speed of numerical mathematics brings in a number
of important new concepts, including conditioning, stability, and accuracy, and efficiency. We will develop these
ideas and learn the most important numerical linear algebra algorithms: QR, LU, SVD decompositions, Gramm-Schmidt
orthogonalization, the QR eigenvalue algorithm, and Krylov subspace methods. Time permitting, we will also study
key algorithms for function optimization and the solution of systems of nonlinear equations.
Text: Numerical Linear Algebra, by Trefethen and Bau, SIAM Press.
instead of 
