Table of Contents
findorbit
findorbit: Newton-Krylov-hookstep search for (relative) periodic orbit of plane Couette flow. Algorithm by
D. Viswanath.
Note: this algorithm can take hours or days to run to completion.
usage: findorbit [-orb|-eqb] [-rel] [-T maptime] [-opts] guess.ff main options: -eqb --equilibrium search for equilibrium or relative equilibrium (trav wave) -orb --periodicorbit search for periodic orbit or relative periodic orbit -rel --relative search for relative periodic orbit or relative equilibrium -T --maptime <real> default == 10 initial guess for orbit period or time of eqb/reqb map f^T(u) -Nn --Nnewton <int> default == 20 max number of Newton steps -Ng --Ngmres <int> default == 40 max number of GMRES iterations per restart -d --delta <real> default == 0.01 initial radius of trust region -sigma --sigma <string> file containing symmetry of relative eqb/orb -symms --symmetries <string> constrain u(t) to invariant subspace generated by symmetries in listed file, arg is filename -R --Reynolds <real> default == 400 Reynolds number -vdt --variableDt adjust dt to keep CFLmin<=CFL<CFLmax -dt --timestep <real> default == 0.03125 (initial) integration timestep -ts --timestepping <string> default == SBDF3 timestep algorithm: (docs to be written) -nl --nonlinearity <string> default == Rotational nonlinearity method: (docs to be written) <flowfield> (trailing arg 1) initial guess for Newton search
The most important options are -orb, -eqb, -rel, and -ax and -az. You use these to specify the kind of solution you are searching for.
- -orb and -eqb are mutually exclusive and you must pick one (search for periodic orbit or equilibrium)
- -eqb leaves the integration time fixed
- -orb adds the integration time T to the search space
- -rel modifies -orb / -eqb, makes the search for a relative periodic orbit or relative equilibrium (traveling wave), by adding finite-time phase shift variables
axandazto the search space - -sigma <filename> sets the initial guess (if -rel) or fixed value (if not -rel) of the symmetry \sigma
- -symms <filename> constrains the search to an invariant subspace. The file is a list of generators for the isotropy group.
In all cases we search for a solution of

where
 \rightarrow s [s_x u, \, s_y v, \, s_z w](s_x x + a_x/L_x, \, s_y y, \, s_z z + a_z/L_z)](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img3fae06af428c8d993696573298cb30b9.png)
(will continue later today…. /2009-06-08 jfg)
Usage examples
equilibrium
Find an equilibrium from initial guess guess.ff
findorbit -eqb guess.ff
traveling wave
Find a traveling wave (relative equilibrium) from initial guess guess.ff, with initial guess for wavespeed
specified in terms of finite shifts (ax/Lx, az/Lz) in finite time T. Equivalent to wavespeed (cx, cz) = 1/T (ax/Lx, az/Lz).
findorbit -eqb -rel -ax 0.3 -az 0.4 -T 10 guess.ff
the –rel option adds the finite shift variables (ax, az) to the search space.
periodic orbit
Find a periodic orbit with initial guess for period T=83
findorbit -orb -T 83 guess.ff
relative periodic orbit
Find a relative periodic orbit with initial guess of a shift by Lz/4 every period T=83
findorbit -orb -rel -az 0.25 -T 83 guess.ff
It takes half a minute's thinking to determine the right -orb, -eqb, -rel, -ax, and -az options based on the type of search you want.
Mathematics
The following is an overview of the Viswanath Newton-GMRES-hookstep algorithm, meant as a reference for the
options of the findorbit utility. It leaves out a number of gnarly details. And please excuse the mishmash of plain text, html, and dokuwiki-latex!
Let
u = discretized velocity field, as difference from laminar flow
f^T(u) = time-T map of the Navier Stokes eqn, numerically integrated
σ = a symmetry of plane Couette flow
G(u,σ,T) = σ f^T(u) - u, a zero of G(u,σ,T) is an invariant solution of Navier-Stokes
r(u,σ,T) = 1/2 ||G(u,σ,T)||^2 = residual of G(u,σ,T)=0
||G|| = a norm of G, to be defined later.
Equilibria, traveling waves, periodic orbits, and relative periodic orbits are all solutions of G(u,σ,T) = 0.
- equilibria: σ is the identity and t is arbitrary. We set σ = 1, hold T fixed to a arbitrary value, and search over u
- traveling waves: σ is a translation τ(cx T, cz T) and T is arbitrary. We hold T fixed and search over u and a finite phase shifts, (ax, az) = (cx T / Lx, cz T/ Lz).
- periodic orbits: σ is fixed and we search over u and T.
- relative periodic orbits: we search over u, σ, and T.
Let x be the finite set of free variables being searched over, e.g. for a periodic orbit, 10^5 spectral coefficients of u plus the period T. We want to find a zero of G(x) or equivalently a minimum of r(x).
Newton algorithm
The Newton algorithm for solving G(x) = 0 is
Let x* be the solution, i.e. G(x*) = 0. Suppose we start with an initial guess x near x*. Let x* = x + dx. Then

Drop higher order terms and solve

Then start with new guess x' = x+dx and iterate.
GMRES
In the present case x is 10^5 dimensional or more, so it is not practical to compute the matrix DG in order to solve the Newton equation. So we use GMRES (Generalized Minimal Residuals), an iterative algorithm for solving linear systems A x = b by repeated calculations of the product A x for test values of x. Specifically, we look for solutions x within n-dimensional Krylov subpaces spanned by Ab, A^2b, A^3 b, …, A^n b. If the eigenvalues of A are well-separated, you can often get a good solution x in a n-dimensional Krylov subspace with n « dim(x).
In our case the product is DG dx, and it is calculated using numerical integration of Navier-Stokes. If x = (u,σ,T), then dx = (du,dσ,dT) and

which can be easily calculated by numerical integrations of f.
For low Reynolds numbers (Re=400) and small cells [Lx,Ly,Lz] approx [pi, 2, pi], we can usually find an
approximate solution to DG dx = -G(x) in forty or so iterations. That means forty or so integrations around
the approximate periodic orbit. This accounts for the bulk of the CPU time consumed by findorbit.
For more on GMRES, see Trefethen and Bau in the References.
Hookstep
Unfortunately, Newton iteration only works when you are very near the solution, i.e. within the radius of accurate linear approximation of dynamics around the solution. Otherwise the Newton step dx can be widely inacccurate and send you shooting off towards infinity (or “to infinity and beyond,” as Beyonce says).
So, instead taking the Newton step directly, we limit the size of the step dx to a trust region
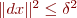
where δ is an estimate of the radius of validity of the linearization about the current best solution x, and we look for the solution to the constrained minimization problem

The Krylov subscript indicates that the norm is the norm of the projection onto the low-d Krylov subspace. It turns out there's a unique, cheaply computable solution to this problem as a function of δ. Call it dx(δ). It has the following properties
- |dx(δ)| = δ
- dx(δ) aligns with the gradient of the residual |DG \, dx + G(x)|^2 as δ → 0.
- dx(δ) equals the Newton step if δ ≥ |Newton step|
- dx(δ) varies smoothly between those values as a function of δ
dx(δ) defines a 1d curve in the Krylov subspace. It is typically a smooth hook-shaped curve parallel to the gradient direction at one end and the Newton step direction at the other –hence the name hookstep algorithm.
Of course, you don't know what the best radius δ for the trust region. The hookstep algorithm uses a few heuristics. It starts with the best δ from the previous Newton-GMRES-hookstep and increases or decreases δ based on the accuracy of the local quadratic model of the residual, |G(x) + DG dx(δ)|^2, compared to the actual residual |G(x + dx(δ))|^2. Each adjustment of δ takes two evaluations of G (i.e. two integrations around the periodic orbit). So the cost of the hookstep adjustment is small compared to the computation of the Krylov subspace and the Newton step.
So, the upshot is this: When you are far from a solution, the hookstep algorithm creeps downhill like a gradient search. When you are near the solution, it switches to the rapidly converging Newton search. It adjusts between these algorithms smoothly, based on its estimate of the radius of validity of the linear approximations in the Newton algorithm.
In pseudo-code, the algorithm is this
start with initial guess x
calculate residual r(x) = 1/2 |G(x)|^2, where G(x) = sigma f^t(u) - u
while residual r(x) is too big and # newton steps < max newton steps {
// Compute Newton-Krylov step dxNewton via GMRES
while GMRES residual > max GMRES residual {
integrate Navier-Stokes to compute DG^n G(x)
find least-squares solution to DG dxNewton = G(x) in n-d Krylov subspace
GMRES residual = |DG dxNewton + G(x)| / |G(x)|
}
while delta (the region of validity of linearization) is uncertain {
compute dxHookstep as a function of delta (cheap)
integrate Navier-Stokes to compute quadratic model of residual, |DG dxHookstep + G(x)|^2
integrate Navier-Stokes to compute actual residual, |G(x+dxHookstep)|^2
if quadratic model is
very accurate: increase delta and try again
inaccurate: decrease delta and try again
alright: break
}
set x = x + dxHookstep
}
References
Divakar Viswanath, “Recurrent motions within plane Couette turbulence”, J. Fluid Mech. 580 (2007), http://arxiv.org/abs/physics/0604062
Lloyd N. Trefethen and David Bau, “Numerical Linear Algebra”, SIAM, Philadelphia, 1997.
Dennis and Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations”, Prentice-Hall Series in Computational Mathematics, Englewood Cliffs, New Jersey, 1983.
Beyonce, “Single Ladies”, http://www.youtube.com/watch?v=8mVEGfH4s5g
