How to find invariant solutions
The channelflow findsoln utility will compute unstable equilibria, traveling waves, and (relative) periodic orbits of plane Couette or channel flows. Here are a few examples of usage.
periodic orbit of plane Couette flow
1. Generate a random velocity field with ''randomfield.''
randomfield -m 0.50 -lx 0.875 -lz 0.6 -Nx 32 -Ny 33 -Nz 32 u0
This will construct a random velocity field in file u0.h5, in a Lx x [-1, 1] x Lz periodic box with Lx = 2 lx pi = 1.75pi and Lz = 2 lz pi = 1.2 pi (the plane Couette minimal flow unit of Hamilton, Kim, Waleffe JFM 1995) with a 32 x 33 x 32 collocation grid (which is a lower resolution than I like for these calculations, but will result in a fast-running demo.) The velocity field u0 will be incompressible and have u=0 BCs at the wall, and will have an L2Norm of 0.50. You can check this by running fieldprops -n u0. I chose this magnitude for the field after testing some smaller fields and seeing that they died to laminar pretty quickly.
2. Integrate the random field forward in time.
couette -T1 1100 -dt 0.05 -R 400 -symms sxyz-sxytxz.asc u0.h5
This will time-integrate the field u0 as a perturbation on top of a laminar base flow U(y) = y for 1100 time units, at Re=400, and with time integration step dt=0.05, and enforcing symmetries in the velocity field specified by the file sxyz-sxytxz.asc By default the velocity field will be saved into a data directory at intervals dT=1. See integration for more information on time integration, such as the base flow plus fluctuation decomposition, or changing from plane Couette to channel conditions.
The symmetry file sxyz-sxytxz.asc has contents
% 2 1 -1 -1 -1 0.0 0.0 1 -1 -1 1 0.5 0.5
That specifies a symmetry group with two generators
![Equations \begin{eqnarray*}
\sigma_{xyz} : [u,v,w] (x,y,z) &\rightarrow [-u,-v,-w] (-x,-y,-z) \\
\sigma_{xy} \tau_{xz} : [u,v,w] (x,y,z) &\rightarrow [-u,-v,w] (-x+L_x/2,-y,z+L_z/2)
\end{eqnarray*}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgebb583fdc13b0c42ea049b2ac04209c3.png)
The pointwise inversion  of this group fixes the origin and prevents traveling waves
and arbitrary relative periodic orbits. For more on symmetry groups of plane Couette flow see symmetry and Gibson, Halcrow, Cvitanovic JFM 2009.
of this group fixes the origin and prevents traveling waves
and arbitrary relative periodic orbits. For more on symmetry groups of plane Couette flow see symmetry and Gibson, Halcrow, Cvitanovic JFM 2009.
3. Select a good initial guess from a recurrence plot.
The  symmetry group allows periodic orbits of the form
symmetry group allows periodic orbits of the form  for
for 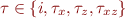 , where
, where  is the forward-time evolution under Navier-Stokes, i.e.
is the forward-time evolution under Navier-Stokes, i.e.  , and where
, and where 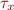 represents a half-box shift in the
represents a half-box shift in the  direction, etc.
direction, etc.
For this demo I'll just look for a solution of the form 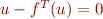 . Thus local minima of
. Thus local minima of 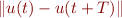 should provide good initial guesses for the search.
should provide good initial guesses for the search.
seriesdist -T0 0 -T1 1000 -dT 1 -tmax 100 -da data/ -db data/ -as -kx 8 -kz 8
This reads in the saved velocity fields from the data directory, computes 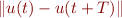 as a function of
as a function of  , and saves this in the file
, and saves this in the file dist.asc. Here's the recurrence plot for the data in question.
You can see strikingly periodic behavior over the range  with nice horizontal blue streak at
with nice horizontal blue streak at  . This suggests the turbulent trajectory is shadowing a periodic orbit with period
. This suggests the turbulent trajectory is shadowing a periodic orbit with period  . The minimum of
. The minimum of 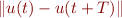 in this region occurs at
in this region occurs at 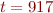 and
and  . That's an unusually promising initial guess for a periodic orbit.
. That's an unusually promising initial guess for a periodic orbit.
4. Find the periodic orbit with ''findsoln''
mkdir findsoln-917-63 cd findsoln-917-63 findsoln -orb -T 63 -dt 0.05 -R 400 -symms ../sxyz_sxytxz.asc ../data/u917.h5
Since I tend to run many searches for many initial guesses, I like to do each search in a subdirectory
named after the initial guess. The findsoln command runs a Newton-Krylov-hookstep search that finds a  solution of the equation
solution of the equation 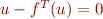 given the initial guess
given the initial guess  and
and  . The search is restricted to the
. The search is restricted to the  symmetry group. The symmetry restriction vastly reduces the search space and results in a faster and more robust search.
symmetry group. The symmetry restriction vastly reduces the search space and results in a faster and more robust search.
After about half an hour the search succeeds, finding a solution that satisfies the equation numerically to  . The characteristics of the search routine are recorded in the file
. The characteristics of the search routine are recorded in the file convergence.asc
%-L2Norm(G) r delta dT L2Norm(du) L2Norm(u) L2Norm(dxN) dxNalign L2Norm(dxH) GMRESerr ftotal fnewt fhook CFL 0.00888606 2.20611e-05 0.01 0 0 0.390225 0 0 0 0 1 0 1 0.609524 0.00663114 1.19704e-05 0.01 -0.0640999 0.0116139 0.38873 0.00902435 0 0.00902435 0.00076865 14 12 2 0.609524 0.000855143 2.14948e-07 0.01 0.190862 0.00429167 0.388192 0.0548914 -0.238276 0.01 0.000119926 29 25 4 0.608904 0.000597692 9.06641e-08 0.01 0.194443 0.00326027 0.387135 0.035679 0.998803 0.01 0.000613148 42 37 5 0.581667 0.000505451 6.2892e-08 0.01 0.18166 0.00364325 0.386258 0.00942818 0.997453 0.00942818 0.000289388 55 49 6 0.583459 1.77901e-05 8.04837e-11 0.01 -0.0438562 0.000824778 0.386507 0.00227387 -0.99388 0.00227387 0.000612772 67 60 7 0.604789 5.46682e-09 8.266e-18 0.01 -0.000571434 1.73752e-05 0.38651 3.13122e-05 0.981989 3.13122e-05 5.95861e-05 80 72 8 0.584728 8.51125e-13 1.58971e-25 0.01 -2.67003e-07 1.49819e-08 0.38651 1.70279e-08 0.940857 1.70279e-08 0.000134271 93 84 9 0.584723 9.72014e-14 2.358e-27 0.01 -1.08282e-10 2.94411e-12 0.38651 5.77394e-12 0.921371 5.77394e-12 0.000331508 106 96 10 0.584723
The solution  is stored in the file
is stored in the file ubest.h5 and the value of  in
in Tbest.asc.

