Table of Contents
Chapter: Continuous symmetries
(ChaosBook.org blog, chapter Continuous symmetries) — Predrag Cvitanovic 2009-02-12
enter the latest posts at the bottom of a section - flows better:
to find recent edits: click on [Recent changes], select changed page, then [Old revision], compare versions
Kuramoto-Sivashinski O(2) quotienting
Ruslan: Predrag, you seem to be enjoying the summer too much: you date the blog entries below as July instead of August. Lucky you, you still have one month of summer left to enjoy. ![]()
2009-07-23 Slice & dice
Predrag: entered Marsden et all derivation of symmetry reduced by slice equations in
thesis/chapters/slice.tex
to RUSLAN: OK, slicing works now in 5-dim, and should work for Kuramoto-Sivashinsky, and I have the reconstruction equation as well. Can you rerun KS in the slice reduced state space? If we are lucky, it might work - if not, we might run into singularities, and have to think again.
Still have not rederived the 'method of connections' (see 'Literature' below). As the frame is 'horizontal' or co-moving, that cannot run into singularities. Nevertheless, it will most likely not be a feasible option, as it requires evaluation of stability matrices ∂v/∂x, and generates additional 'geometric phases.'
2009-07-24 Slice & dice
Ruslan: Do you expect that a RPO of KS will become a periodic orbit within the slice if we integrate Eq. (66)?
Predrag: yes (here (66) is Siminos thesis day's number of the slice flow equation)
Ruslan: Do you also expect that Eq. (65) will give us the RPO shift if we integrate it over the RPO period?
Predrag: yes (here (66) is the reconstruction equation for reduction by the slice)
Predrag: We got it to work for complex Lorenz. I would take for x^* some 'random' seed: 0 in the first component, random numbers in the rest, to make sure on is not in a subspace. That was presumably the problem with the first try, when Vaggelis fixed the angle in the (x_1,x_2) plane, which happens to be 2-dime rep of SO(2).
The thing that worries both Vaggelis and me is that there is no reason why the flow should not cross
(Tx).(Tx^*)=0
subspace every so often. If it does, singularity is not so bad, essentially (I believe)
d \theta/dt = sin \theta/ cos \theta
so one can either continue through it in the complex plane, or switch to a new slice and then switch back to initial slice once crossed. But that is a bit of a pain, hope we can avoid it.
I would test the code by
- running with relative equilibria as initial conditions
- running with periodic and relative periodic orbits as initial conditions
Ruslan: The singularities are the least of my worries. I think there is something fundamentally wrong with applying this approach to PDEs defined on a periodic domain. Since KSE is too difficult for me to understand, I'm now working on an example of a much simpler dynamical system where I can see what's happening. I'm writing it in Vaggelis's siminos/blog. Will hopefully commit by the end of today…
Predrag: The main trust of the two Rowley-Marsden papers cited below is applications to PDEs. They POD traveling waves, so if it works for them, should work for us. For a more pedestrian derivation, consult Rebecca Wilczak's project
Ruslan: I don't doubt that it will work for the traveling waves and also for slightly modulated traveling waves. In this case the dynamics on a slice is a fixed point or an orbit meandering in a small neighbourhood. Since this neighbourhood is small, the group action tangent is not changing much, so everything works out OK. I think I now understand why it will not work for general RPOs: it is because the topology of the slice can be very complicated, so, if the orbit on a slice moves around a lot, it can re-emerge at the same point through many different routes. I'm trying to illustrate it on a simple examle in siminos/blog. Stay tuned…
2009-07-25 Eurosceptics do not like to slice
Ruslan: check siminos/blog/blog.tex - one gets a phase shift by \pi if one crosses the singularity
Predrag: Your model illustrates why we need monotonicity in phase (we are integrating 1d equation, velocity cannot change sign?). But I think we will fix it - it is like WKB for harmonic oscillator, one gets geometric \pi phase for each turn, and a neat way to do it is Maslov trick - change slice at pi/4, then change back at 3\pi/4, etc. Looks like something we can figure out. Sure cute - getting semiclassical Keller-Maslow phase without doing neither wave nor quantum mechanics. At least, not consciously.
More interesting will be the phase for the method of connections. If we are lucky, it is the same for relative periodic orbits.
Vaggelis: Apart from quantum mechanics there are classical systems that exhibit such behavior, see for example http://prl.aps.org/accepted/L/cf079Ya5Q7f19828e08c7183313c1d9b2e9126ce4 . I've only seen it in Hamiltonian systems, where this behavior is called monodromy since one studies the system as it goes once around a singularity (is the etymology clear to non-Greeks too?). It apparently arises when a function fails to be single-valued, which again should point out why we need monotonicity in phase.
Question for Ruslan: Is it really trivial to deal with the singularity at  ? You still need to cover the reduced space with more than one coordinate systems which is essentially the same as choosing a new slice. Even if this doesn't bother us, I am afraid that we will get projections that are not more informative than Figure 42 in todays version of my thesis, where the singularity was dealt with but
? You still need to cover the reduced space with more than one coordinate systems which is essentially the same as choosing a new slice. Even if this doesn't bother us, I am afraid that we will get projections that are not more informative than Figure 42 in todays version of my thesis, where the singularity was dealt with but 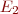 and
and 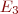 collapse to the same point.
collapse to the same point.
Ruslan: I'm moving this discussion from here to siminos/blog/blog.tex
2010-01-04 On choosing the slice point for PDEs
Predrag: I'm skipping siminos/blog/blog.tex for this post, in order to get to plumbers as well, not only Eurosceptics. The gist of it should go into ChaosBook.org chapter Continuous symmetries, but I'm very slow entering edits.
There I already show that the denominator in the reconstruction equation is given by the quadratic Casimir for the representations involved. For SO(2)-equivariant flows (KS, pipe streamwise translational invariance on a periodic cell) this means that (asymptotically) mth Fourier mode magnitude must be less than 1/m. If all modes are kept under 1/m in magnitude, the diseases noted by Ruslan go away. (Ruslan noted that if m=2 dominates over m=1, symmetry reduction does not reduce relative periodic orbits to periodic orbits.)
Flow crossing the vanishing of phase-velocity denominator at an instant in time is innocuous, as we know how to cross that point by the method of (finite time step) moving frames.
However, if slice point has no component in the mth subspace, but this is a flow-invariant subspace, the phase-velocity denominator is and remains identically zero. Hence one must make sure that the slice point has non-vanishing components in ALL invariant subspaces, ie., Cm. My initial suggestion of using a nice traveling/rotating wave to fix the slice is not good (neither is Ruslan's fixing of m=1 Fourier mode, failing that m=2 Fourier mode, etc.). My suggestions:
- simulate turbulent state, measure the average magnitude of mth Fourier mode (for KS we know it is falling off like 1/m^4 already).
- try to construct a slice point with all Fourier modes nonzero, and roughly of the magnitude seen in the turbulent state.
- perhaps 'freeze' an instant in the turbulent evolution, with roughly right Fourier component magnitudes. That would be good for experimentalists, as that is the only slice point choice we can get from the raw time series.
John Gibson This so nicely spans both my intimate knowledge and my vast ignorance that I feel compelled to actually read your slicing and dicing work. The question I take into it is whether the analysis survives expansion to multidimensional spatial domains and tensors products of 1D Fourier and non-Fourier modes. E.g. in a channel flow the mth Fourier mode in x is a 2D function of (y,z), not a complex number. So it is not necessarily straightforward to translate “when the mth Fourier mode passes through zero”. However I made up that quote rather than finding it in your writing, and everything you say here seems to be generalizable. We all know where the devil lives; I will have to go knock on his door and explore his house.
2010-01-06 Predrag For our PDE work I always use real 2D representation for Fourier modes, so we are on the same page. Group theory (Schur Lemma?) says that in defining an L2 product I am only allowed to use [2×2] identity multiplied by a constant on each such 2D linearly irreducible subspace, once for spanwise, once for streamwise, and no wall-normal symmetry reduction, other than what is included in discrete reflections. Give my best to the devil, tell him we got the message: if there is a symmetry, USE IT (long-winded version), or, JUST DO IT! (wisdom of Vaggelis T-shirts). If you check Siminos blog, for KS relative periodic orbits are starting to get reduced to periodic ones, and you can see what happens to slicing if higher Fourier coefficients of the slice point are too big in magnitude.
A co-moving frame is not the answer
Predrag 2010-04-22 writes to Carles Simó We've been arm-wrestling for a year now with continuous symmetries, more precisely how to go effectively to reduced state space M/G, where G is a continuous symmetry of dynamics (typically a compact Lie group such as O(2) X SO(2)) and M is extremely high-dimensional state space, such as a Navier–Stokes fluid). I think it would be simpler to do this first for dissipative, rather than Hamiltonian flows. Symmetry reduction has to be a post-processing method, as nobody is going to rewrite DNS code just to make me happy, and has to reduce a large set (for KS we have 40,000) of very different relative periodic orbits in M to periodic orbits in M/G. We have not find Marsdenise helpful. If you have a smart method how to do this, let me know?
Carles Simó If you have something that seems to be a periodic orbit in some rotating frame, I would suggest to find the “rotation of the frame” (frequency analysis, e.g., can be helpful), undo the rotation at the end of the period and try to obtain the “clean” p.o.
Predrag A co-moving frame is helpful in visualizing a single ‘relative’ orbit, but useless for viewing collections of orbits, as each one drifts with its own angular velocity. So we gave up on that early on. Visualization of all relative periodic orbits as periodic orbits we attain only by global symmetry reductions. We do it by “slicing”, ie finding hypersurfaces that cut group orbits just like Poincare sections cut time-evolution orbits. The problem is that the natural choice;a hyperplane normal to a group orbit tangent vector (Lia algebra generator) is only good locally, globally it runs into singularities.
Ginzburg-Landau system with SO(2) x D_4 symmetry
Predrag 2010-06-05 Calling an overall complex phase “gauge invariance” is a waste of an ugly but otherwise quite precise word. In quantum field theory one means by that the local gauge invariance (a very deep concept) in the original sense of Weyl, not the relatively trivial global gauge invariance. That is why in our papers and in the ChaosBook.org we never refer to “gauge fixing” when we discuss the choice of a slice, even though it is a method for fixing the phase of solutions. I'm saving the word for the tough, local “gauge invariance”, if we ever get back from the classical PDEs to the quantum field theories. But AMO physicists do indeed use “gauge invariance” also for a global symmetry.
Daniele Avitabile 2010-06-05 Our problem has SO(2) x D_4 symmetry. What we would like to achieve is exploring the symmetry-breaking bifurcation scenario pertaining to D_4, in the case of stationary solutions. In other words, we do not want to simulate the time-dependent solutions of the Ginzburg-Landau system. We concentrate instead on stationary solutions, and we want to see how, by breaking D_4, we can get new, hopefully observable, steady states.
Predrag I think that you get equilibrium solutions only within subspaces fixed by D_4 symmetries. The should be also SO(2) travelling wave solutions, perhaps also important. They would come in two flavors - with irrational velocities, and pre-periodic, belonging to a discrete C_m subgroup of SO(2). And you can bifurcate into Hopf cycles, traveling waves, periodic orbits, relative periodic orbits etc., unless for some reason the physics does not like anything time-dependent.
Daniele In order to do that we need to factor out the continuous group symmetry SO(2). As far as I understood from your comments, we should be careful in doing that, as the the phase condition that we chose now (seeking a solution in a hyperplane normal to a group-orbit tangent vector) is valid only locally. Am I correct in interpreting your statement?
Predrag Yes. Though these singularities are perhaps easy to deal with…
Daniele If so, I should say that we explore our stationary solutions only by means of numerical continuation. With this method, the best we can do *is to search locally*. What we need to make sure is that, once we have a solution and perturb it, we can still invert our problem and find a new steady solution. In other words, seeking for a solution locally is the best we can do, as far as I can tell. Do you think we could be missing some patterns by using our phase condition? I think your observation would be absolutely crucial if our continuous symmetry group was acting on the time-variable as well, and we wanted to simulate them. A typical case would be continuing time-dependent patterns like spiral waves or scroll waves. A method that comes to my mind in this context is the Freezing method by Tuemmler and Beyn, which you will probably know. I am pretty sure that this differs from the slicing method that you told us about. A recent article by Hermann and Gottwald recaps the method and contains an extensive set of references about it.
Predrag I have read Tuemmler and Beyn and believe “freezing” = “slicing”. Siminos and I have Hermann and Gottwald on our reading list, but have not studied it yet. Tuemmler and Beyn impose a slice by adding a new dimension (the phase parameter) and a condition (a Lagrange multiplier), while we go one dimension down by restricting the dynamics into the slice. Both approaches are standard in imposing Poincarė sections; Rytis Paskauskas have written that up for Chapter 3 - Discrete time dynamics (not yet on the public version), and Chapter 13 - Fixed points, and how to get them, Section 13.4 Flows. My feeling is that Tuemmler and Beyn is better, but we have not implemented it. If you do use it, let me know how it works.
Daniele Now, let us assume that we manage to factor out SO(2), either locally with our phase condition, or globally via the slicing method. You mention that you always quotient discrete symmetries. Would you recommend this in our case? What is the danger in not factoring them out? My gut feeling is that, by factoring D_4, for instance, we will make sure that we will find just one solution on the group orbit. I don't think this is bad in general, and I would be pleased to learn what are the problems associated with it.
Predrag The quantum mechanics and the periodic orbit theory (see Chapter 21 - Discrete factorization) demands that discrete factorization be implemented - anything else would be stupid. Finding only 1 solution on a group orbit is not “bad”, it's actually just great - and you can always return to the full state space by generating other solutions by the group actions.
However, getting one's students to do it is another story - the light goes on only after one has tried to use the periodic orbits one way or the other way (or tried to compute something in quantum mechanics with and without performing symmetry reduction first). People like to stick to full space, as discrete symmetry makes humanly “nicer” pictures, just like a kaleidoscope does.
As far as I know, there is no price paid for reducing discrete dynamics (going from the full state space to a fundamental domain that tiles it) other than thinking.
Remarks
2010-01-12 Dwight Barkley Seems like a big pain to work through history. Would be easier if you waited until the participants were dead, don't you think? They can't complain then anyway.
2010-01-12 Predrag Price one pays for being Teutonic. The problem is - who dies first? More of the problem is that I'm still crying out for help - I'm sure slicing can be done better for KS, spiral and fluid dynamics than what I have learned so far, so I'm hoping from enlightement from somebody from this wise crowd, so I'm trying to stay straight and narrow. If I do not mention them, they'll surely complain…
Literature
![]() Two continuous symmetry reduction papers of interest:
Rowley and Marsden 2000 and
Rowley et.al. 2003. The procedure looks like a trick Arnol'd suggests in “Ordinary differential equations” book, section $6.2. It works “locally” but how are the pieces glued together? — 2009-02-22 16:20
Two continuous symmetry reduction papers of interest:
Rowley and Marsden 2000 and
Rowley et.al. 2003. The procedure looks like a trick Arnol'd suggests in “Ordinary differential equations” book, section $6.2. It works “locally” but how are the pieces glued together? — 2009-02-22 16:20
 Notes on Rowley and Marsden 2000:
Notes on Rowley and Marsden 2000:
The main result is a method for the reconstruction of traveling KL modes from their corresponding symmetry-reduced modes by finding reconstruction equations for the relative equilibrium moving frame variable  . This is applied to KL (or POD) long time averaged data, in cases where the average drifts with a constant velocity
. This is applied to KL (or POD) long time averaged data, in cases where the average drifts with a constant velocity  .
.
In the geometric phase literature one gets dynamical equations on the phase space modulo the symmetry group (these are called the reduced equations on the reduced phase space) and the problem is then how to put back into the dynamics the missing group, or phase variables. These additional equations are usually called the reconstruction equations.
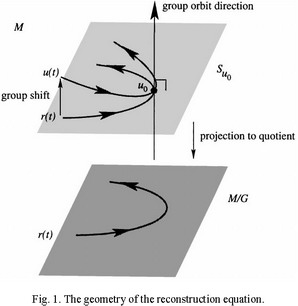 Whenever one has equivariant dynamics on M, one gets a well-defined dynamical system on the quotient (or orbit) space
Whenever one has equivariant dynamics on M, one gets a well-defined dynamical system on the quotient (or orbit) space  which consists, in our case, of the space in which two functions related by a translation are
identified. When M is an inner product space and the group action is by isometries, there is a natural way to identify,
at least locally in function space, the quotient space with a subspace of M; namely we pick a point
which consists, in our case, of the space in which two functions related by a translation are
identified. When M is an inner product space and the group action is by isometries, there is a natural way to identify,
at least locally in function space, the quotient space with a subspace of M; namely we pick a point  and
look at the affine space through the point
and
look at the affine space through the point  orthogonal to the group orbit through that point.
They call this affine
space a slice and denote it by
orthogonal to the group orbit through that point.
They call this affine
space a slice and denote it by  . This is precisely the same as Predrag's request that reduced equations be obtained by projecting out the component of velocity field that points along the group theory orbit.
. This is precisely the same as Predrag's request that reduced equations be obtained by projecting out the component of velocity field that points along the group theory orbit.
 Notes on Rowley et.al. 2003:
Notes on Rowley et.al. 2003:
 The “Geometry of the reconstruction equation” figure illustrates the method of 'slices,' where group orbits are sliced by normal planes fixed globally. Reduction to M/G reduced phase space runs into singularities (cf. our papers on symmetry reduction, Siminos thesis, ChaosBook.org/projects/Wilczak), presumably one needs a set of slices to cover all of the state space. Predrag's proposal to quotient out the group direction locally, at each point along the full state-space trajectory is called the 'method of connections' and necessitates a computation of a 'geometric phase,' as relative periodic orbits do not become periodic orbits in the state space so reduced. — Predrag Cvitanovic 2009-08-17 02:34
The “Geometry of the reconstruction equation” figure illustrates the method of 'slices,' where group orbits are sliced by normal planes fixed globally. Reduction to M/G reduced phase space runs into singularities (cf. our papers on symmetry reduction, Siminos thesis, ChaosBook.org/projects/Wilczak), presumably one needs a set of slices to cover all of the state space. Predrag's proposal to quotient out the group direction locally, at each point along the full state-space trajectory is called the 'method of connections' and necessitates a computation of a 'geometric phase,' as relative periodic orbits do not become periodic orbits in the state space so reduced. — Predrag Cvitanovic 2009-08-17 02:34
 Found some literature on symmetry reduction in field theories:
Found some literature on symmetry reduction in field theories:
- A. Jadczyk, Symmetry of Einstein-Yang-Mills systems and dimensional reduction. Would be lovely to get back to the that… — Predrag Cvitanovic 2009-12-17 23:17
- Cesare Tronci, Hybrid models for complex fluids. Need to have a look at Vlasov-Yang-Mills systems. — Predrag Cvitanovic 2010-11-22 07:12
~~DISCUSSION~~
