Table of Contents
2009-06-12
I am starting work with Tobias Schneider on spatially localized solutions of plane Couette flow. These solutions were found by Daniel Marinc in his master's thesis under Bruno and Tobias, with edge-state searches in several different large aspect ratio simulations. Interestingly, they seem to unite with spatially periodic solutions under continuation in Re. My first step is to recalculate these continuations and reproduce the connection. Below are a continuation diagram and several plots of the localized equilibrium state at different Re. Note how the localized solution spreads out to the whole domain as Re goes from 200 to 160. The continuation is still running; I will update as more data comes in.
(continuation figs updated 2009-07-8)
2009-07-07
Eigenvalues as function of Reynolds number for the spatially periodic solution, computed for (Lx, Lz) = (4 pi, 8 pi), i.e. four spanwise repeated copies of one spatially periodic state (the Re=150 plot above gives you the picture). The two plots below show the real part of the leading eigenvalues versus Reynolds number. Left: the 10 leading eigenvalues, sorted and colored by magnitude of Re λ. Right: The eigenvalues that cross the real axis, remixed so the color stays continuous as the eigenvalues cross.
Note:
- Many eigenvalues are repeated and/or complex, thus fewer than ten lines appear in the left plot.
- The leading eigenvalue (black in the left plot) is isolated.
- The next eigenvalues (red/blue in the right plot) are doubled.
- In the regions where red and blue are distinct, each red line shows two real eigenvalues (same for blue).
- Where blue overlaps red, we have two equal complex pairs.
- The doubling of eigenvalues corresponds to a half-cell phase shift in the eigenfunctions. (I am pretty sure of this but haven't confirmed it by inspection).
The real eigenvalues crossing at Re=150 produce the spatially localized state shown in velocity-field plots above. The complex eigenvalues crossing at Re=143 should produce a traveling wave, standing wave, or periodic orbit. I am puzzled by the lack of further bifurcations at Re=150, since Tobias mentioned (I think) that many localized states bifurcate off at Re=150. But maybe you can produce many solutions around Re=150 by appropriate linear combinations of the independent phase-shifted eigenfunctions. Need to talk to Tobias about this and read up on simpler cases. John Gibson 2009-07-07 16:03 EST
Tobias Schneider 2009-07-07
Hi John,
looks great!! We should definitely talk soon - I'll try to reach you tomorrow - today I was unfortunately so busy with talks and administrative stuff that I could not respond to your mail - sorry for that.
Brief comment on the expectation of many solution bifurcating from the non-localized one: What we observed is, that at Re=150.2 (btw. what is your stepsize in Re?) there are at least two solutions connecting to the periodic one. One is the localized slowly moving traveling wave that is the edge state at Re=400 (and has a single unstable direction at 400). This solution is invariant under s_z (see page 65 of Daniel's thesis for the exact definition). (it is an even solution as a function of spanwise coordinate when averaged in streamwise solution). The other solution is the localized fixed point that is invariant under s_{x,y,z}. Can you try to also follow this solution down in Re to check how it connects to the periodic solution?
That there should be more solutions bifurcation at the same point is probably not true. It would be the case, if we are looking at the 'lower' connection of the snaking curve with the periodic solution. However, I think we study the point where the snaking curve 'reconnects' to the periodic branch due to periodic boundary conditions. I guess, our domain is simply not wide enough to show a real turning around of the snaking curve. Would it be possible to take the localized solution (either the tw or the fixed point - the best would of course be both) at a point where they are well localized (say Re=300) and put them into an even wider box. To minimize interpolation errors in a box twice or if possible even 4 times as wide. Assuming that your code allows to detect saddle-node bifurcations and to follow them 'around the corner' we might get a full snaking that way.
Let's talk about that in more detail. Are you in town next week - I would really like to schedule a meeting both with you and John Burke - we could either meet at Harvard or also visit John at BU.
Best, tobias
John Gibson 2009-07-09
By the way, I am worried that the localized traveling wave solution might be spurious. The residual at the given resolution is 1e-14 or so, but I cannot get better than 1e-06 at any other resolution. E.g. I transfer from Nx,Nz = 64,128 to 64,144, then the residual goes up to 1e-05, and I can't reduce through Newton-Krylov. The globally periodic solution shows no such problem.
2009-07-13
Continuation of localized solution on larger domain. The results above are for a localized solution on a 4pi x 2 x 8pi domain. Note that as the localized lower-branch solution is continued down in Re, it starts to fill the whole box and merges into the globally periodic lower-branch solution around Re=150. Tobias suggested putting the localized solution in a larger box and seeing if it would then continue around a saddle-node bifurcation to give us a localized upper branch. Good news: it does!
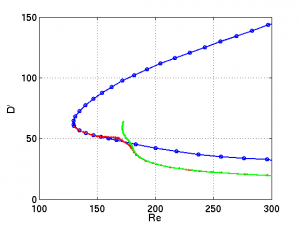
These plots show dissipation versus Reynolds numbers for three equilibrium solutions: the “global eqb”, a solution that is triply periodic in the (4pi,2,8pi) box (see Re=150 plot above),for which we have both upper and lower branches; the localized solution in (4pi,2,8pi) box (see Re=400 to 150 plots above); and the localized solution fit into a larger box (4pi,2,16pi) (shown below). I'm using a different definition of dissipation here because including the laminar dissipation and normalizing by volume obscures the fact the localized solutions in the two different boxes are almost identical from Re=400 down to Re=190. The definition of dissipation here is

compare to the usual

so D' = Lx Lz (D-1).
The computation is pretty slow, because the grid is large 32 x 33 x 384 for (4pi,2, 16pi). This discretization was appropriate for the localized lower branch at Re=400 but looking at the spectra 48 x 33 x 256 would be more appropriate for solutions near the saddle-node.
skype chat: [12:11:50] tobias.schneider: Hi John - does the solution after the turn show an additional pair of streaks? [12:12:57] John F. Gibson: Yes. The ones on the ends strengthen. There are plots on my blog now; annotation still coming. [12:13:16] tobias.schneider: cooool!!! I really think that this is a major breakthrough - a saddle-node bifurcation that gives an additional pair of streaks!!! We have indead a snaking bifurcation! … [12:19:56] tobias.schneider: perfect - if you have enough time to do that - could you try to also plot the spectra at the saddle node bifurcation point - that would be great [12:42:20] John F. Gibson: I will try to do that by the time we meet John Burke. These computations are slow!
2009-07-14
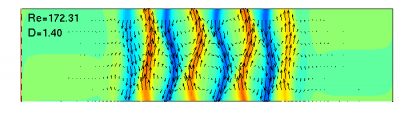
I found another localized solution by a simple modification of the existing solution (examined above). Let EQa be the existing solution. It's pictured below at Re=173.25. In the interior there's a pattern that repeats itself. I spliced out one copy of that pattern to produce EQbguess2 and then ran Newton-Krylov hookstep to get the new solution EQb. The picture of EQb is shifted a little to the right in z in order to center it, approximately.
I started a continuation of EQb to add to the D' versus Re plots. Also, it looks like one pattern could be spliced out of EQb as well, so I did that (EQcguess) and have a search running on that. I did a crude job on splicing, merely copying gridpoint values of velocity from one field to another, and taking a jump of one pattern length (plus or minus the gridspacing Delta z) in the middle. This messes up the continuity of the solution, induces Gibbs phenomenon, and gives non-zero divergence. Rather than spend time doing a better job I just time-integrated the crude guess for few time units until the Fourier spectrum adjusted (killed high-order modes). This zeroes the divergence as well. It seems to be good enough.
Update: Oops! EQb is the same as the lower branch of EQa. So no new solution. I guess this is how snaking bifurcation works…. you go around a saddle-node and gain/lose one copy of the pattern. I am continuing with the EQc guess because it would have one less copy than EQa's lower branch and so presumably be altogether different, if it converges without changing too much. We'll see.
Update 2009-07-15 EQcguess converges to the lower branch of EQa as well. Its tails grow under Newton-Krylov iteration.
2009-07-15
Updated continuation plots. The Back to the usual definition of dissipation, including laminar and normalized by box volume. This will be better to show the snaking connections to the globally periodic solution.
These fields are points on the green curve. All are for 4pi,2,16pi.
Resolution These computations are expensive enough that it's worthwhile finding the minimum acceptable resolution. I recomputed the Re=174.36, D=1.484 4pi x 2 x 16pi localized solution at variety of resolutions. Spectra and properties of solutions are shown below.
The quantity shown in the Fourier spectrum is
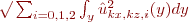
In my experience six orders of magnitude between largest and smallest Fourier coefficients is a pretty solid guarantee of stability of solutions under increasing resolution. The Chebyshev spectrum shown is

as a function of ky for a few of the lowest-order values of (kx,kz).
| grid | D | init | final | feval | minutes |
| 24 33 128 | 1.505 | 3e-04 | 3e-05 | 216 | 059 |
| 32 33 192 | 1.48302 | 2e-05 | 2e-15 | 149 | 067 |
| 32 33 256 | 1.48401 | 4e-06 | 2e-15 | 108 | 066 |
| 32 33 384 | 1.48393 | 4e-06 | 1e-13 | 129 | 114 |
| 32 49 256 | 1.48401 | 4e-06 | 2e-15 | 112 | 122 |
| 48 33 256 | 1.48397 | 8e-06 | 4e-15 | 112 | 174 |
| 48 33 384 | 1.48390 | 8e-06 | 2e-14 | 099 | 231 |
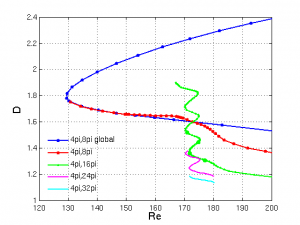
32 x 33 x 256 for 4pi x 2 x 16pi seems to be the sweet spot. To get a few rungs on the snaking ladder, I am starting continuations of the localized solution on boxes with Lz = 24pi and 32pi, with Nz = 384 and 512 respectively.
2009-07-16
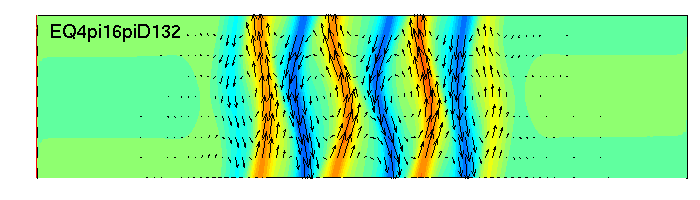
A few more rungs on the ladder in the 4pi x 16pi box (green) and a few points on 4pi x 24 pi (magenta) and 4pi x 32pi (cyan). I've marked a few spots on the 4pi x 16pi curve that show corresponding points on successive rungs of the ladder. Midplane velocity fields for those solutions are shown below. Tobias, John, please add comments to remind me what we are looking for between successive rungs.
 Warning: all these should be labeled 4pi x 16 pi!
Warning: all these should be labeled 4pi x 16 pi!
BTW, I've confirmed that the globally periodic solution is the same as the Nagata lower branch EQB, by continuing down one copy from 4pi x 2pi to 2pi/1.14 x 2pi/2.5, for which I have the Nagata EQB.
Yikes! I've been off by a factor of two on my box sizes through most of this discussion! I went back and changed all the values in the text but some figures have box sizes in labels. I won't change those; it's too much trouble. Box sizes in figures above this point should be doubled, below this line they are correct.
Also, the only symmetry satisfied by this solution is s_xyz, where s_xyz : [u,v,w](x,y,z) → [-u,-v,-w](-x,-y,-z), with a suitably chosen origin. I've checked in detail. The globally periodic solutions have more symmetries, due to the possibility of combining phase shifts with s_z : [u,v,w](x,y,z) → [u,v,-w](x,y,-z) and s_xy : [u,v,w](x,y,z) → [-u,-v,w](-x,-y,z).
2009-07-18
Further progress on continuing solutions in 4pi,16pi and 4pi,24pi.
Some comments on computation. After determining the symmetries of the solutions I optimized the phase shifts in x,z so that the center of symmetry is exactly (0,0) or equivalently (Lx/2, Lz/2) and also made sure the solutions were in the same orientation about the center. We had a brief power outage last night that caused my machine to reboot; this gave a good opportunity to restart the computations with the optimized phase shift, with sxyz symmetry enforced during time integration and continuation, and with the continuation program set to give up and try a smaller continuation step if the Newton-search steps are poor enough that the trust-region hookstep mechanism kicks in. Observations suggest that continuation is more efficient in total computation time if we never leave the convergence region of pure Newton iteration. Also, I reduced the discretization of the 4pi,16pi continuation to 32 x 33 x 256.
I started Arnoldi iteration on the phase-shift optimized versions the previously calculated solutions for 4pi,16pi. I didn't want to start these without symmetry optimization, since I need to examine symmetry to sort the eigenvalues, and it's a lot easier to detect the symmetry of the eigenfunction if you know the center of symmetry of the solution. That's running now. Looks like about an hour per solution at 100 Arnoldi iterations per solution. With two CPUs going and about fifty solutions (every other dot on the green curve), it'll take 24 hrs or so. It's clear from the first calculation that 100 Arnoldi iterations is not overkill. The first calc is at the 66th iteration, and the second zero eigenvalue is not yet resolved well enough to distinguish it clearly from the small non-zero eigenvalues. Arnoldi iteration generally requires more iterations to get accurate eigenvalues than GMRES does to get an sufficiently accurate solution. No great accuracy is required in GMRES solutions to Newton steps, since the Newton procedure is iterative itself.
2009-07-20
Further progress on continuing the localized solutions 4pi,16pi and 4pi,24pi. 4pi,16pi appears to be headed to the upper branch of the Nagata solution. The Arnoldi iterations are still cooking. I had to restart them with a longer integration time (T=20) for the finite-time map u-f^T(u) in order to get better separation of the eigenvalues near zero. I've set up a bash script to do Arnoldi iteration on every other data point in the 4pi,16pi continuation; those should finish today, and then maybe I'll start it on the intervening points. Following that I'll have to solve the bookkeeping problem to track individual eigenvalues between continuation steps. In the meantime I'm going to work on some Poincare sections that have been stalled for some time…
BTW, the limiting factor on these computations is going to be memory in the Arnoldi iteration. The algorithm requires an LU decomp of an M x N matrix, where M is the number of independent spectral coefficients in the discretization of the velocity field, and N is the number of Arnoldi iterations. For the 4pi,16pi box with 32 x 33 x 256 gridpoints, that's a 200,000 x 100 matrix, and the process size gets to 1.2 GB during the LU decomp. My machine has 4 GB DDR3 1600 RAM and 4 cores, so I can do a couple Arnoldis at a time without trouble. But I expect to hit my upper limit pretty soon (a factor of 2 or 4) in domain size or Reynolds, or even sooner with less smooth solutions, which will need finer resolution. The Nagata LB is unusually smooth. I could put in two more 2 GB sticks to move up to 8 GB RAM, but then I'd have to downclock the RAM to 1033. I think the PACE machines are all 4 GB.
2009-07-22
An updated plot of the continuation is just above. The resolution is getting closer to borderline, so I'm spot-checking a few datapoints at 48 x 33 x 384. Arnoldi iterations continues as well. So far I have eigenvalues for 4pi,16pi from (Re,D) = (180, 1.28) to (172, 1.84) at every other datapoint. To deal with the eigenvalue dataset I will have to solve some bookkeeping problems; right now I am deferring that problem for a few days to work on other things.
2009-07-23
(left) Volume-normalized dissipation, (right) dissipation without volume normalization.
The 4pi,16pi solution at (Re,D) = (176.59, 2.09).
The localized solution does not appear to be headed towards N copies of the Nagata upper branch quite so simply. Portions of the midsection velocity-field plot above shows a distinct diagonal symmetry, i.e. u(x+lx, y, z+lz) = u(x,y,x). I imagine that we could get perfect diagonal symmetry by adjusting the box size Lx,Lz to fit the observed lx,lz. Maybe this can help us understand the diagonal fronts in turbulent spots in plane Couette flow (this and a lot more work).
(TMS) It is also known in SH in a periodic domain that the localized solution can reconnect to different periodic ones - but I have to check that. Let's ask John (B.) about that. I like the idea to somehow relate that symmetry to the tilted stripes in fully extended pCf - let's think and talk about that!
TMS 2009-07-23
Meeting notes
So - let's try if I manage to use this `common notepad':
As promised a few keywords summarizing the discussion on 2009-07-15. The keywords are ordered according to the three goals of that research that we discussed.
1. Demonstrating snaking behaviour in pCf:
(Short term project, almost done! John, you are great!!!)
Approach: Follow the snaking curve by continuation of the localized solutions (both the fixed point and the traveling wave) in a larger computational domain.
Saddle-node bifurcations at 'turns':
- Compute spectra to demonstrate that we have saddle-node bifurcations.
- Compute relevant eigenfunction: Should be of the SAME symmetry and 'add' a pair of streaks on both sides (growing mechanism).
- Redo the same for the traveling wave of opposite symmetry (thus we get the two (or even four - if one does not identify solutions which are reflected at the midplane) localized branches the system seems to allow for)
Ladders of the 'Snake & Ladder structure':
- Search for additional bifurcations close to the saddle-node bifurcation (in SH the additional 'symmetry-breaking bif.' moves closer to the saddle-node bifurc. as we move up the snaking curve). The eigenfunction here should break the symmetry. Thereby the 'ladder branch' can connect the even and the odd snake. NOTE: I expect the eigenfunction branching off the equilibrium we already have to be a traveling wave that slowly drifts in downstream direction (the solution is dragged with one of the walls as the up-down symmetry is broken). That also means that the symmetry breaking solution comes in a pair (one moving in +x and one in -x direction).
Additional questions:
- Check streak spacing (wavelength) of the solution along the snaking curve. Aim: Understand 'breathing' and wavelength selection.
- Drift of the even solutions also in SPANWISE direction? Cp. to the 'pumping' of localized solutions in convection.
- Reconnection point (reconnection to the periodic solution) as a function of domain size.
- Check features of the bifurcation at the reconnection point (essential for project 2). Expect.: Long-wavelength instability (eigenmode should have the full wavelength of the computational domain).
2. Generate a 'gallery' of localized exact solutions.
Aim: Transitional turbulence as a (random) walk between many unstable exact solutions also captures localized turbulence in spatially extended systems. (Dream: Redo John's and Predrag's state space analysis: heteroclinic connections, long periodic orbits…..)
Approach: Compute localized versions of known periodic equilibria by detecting the bifurcation where the localized solution reconnects to the periodic one due to the periodic bc of the computational domain.
- Connection either at the upper OR the lower branch → search along both branches starting form the saddle-node bifurcation of the periodic solution. Detection: EV crosses the real imag. axis AND eigenfunction has only the periodicity of the full computational domain.
- Try automatic search algorithm with known solutions. (Study spetrca at the various reconnections that you are computing right now)
Note: Not all of those solutions are expected to undergo snaking!!!!
3. 'Guessing' and effective amplitude equation describing localizsation in pCf:
Idea: Simplified equation (complexity similar to Swift-Hohenberg) that captures the localisation mechanism and allows for an analysis of the full bifurcation structure. Hope/dream: equation might predict features such as a the typical size of the exact solutions as a function of Re (might be possible if we generically find slanted snaking).
Approach:
- Collect features of the computed solutions (symmetries,…) and try to 'reverse engineer' the amplitude equation.
- Compute relative strength of the various terms in the Navier-Stokes operator for the localized solutions → what are the important terms?
- Note: An equation for a single scalar order parameter (such as kinetic turbulent energy) as tried for many years by the phase saparation community cannot work!! Reason: The equation has to be at least 4 dimensional considered as a spatial dynamical system. Since the Laplacian in Navier-Stokes is only of second order, we need at least two coupled scalar fields (such as two averaged velocity components). I know that this is a difficult task and many bright people have tried to wirte down an effective euqtion for turbulence in the last decades - however, I guess all have tried to use a single order parameter - let's see if we can do something!
PLEASE: Both Johns ![]() : Feel free to add ideas / comments. John (G.): You can also move those more general ideas to a separate page - whatever seems to be best for you.
: Feel free to add ideas / comments. John (G.): You can also move those more general ideas to a separate page - whatever seems to be best for you.
2009-07-27
Thanks for the meeting summary, Tobias! Here are the snaking continuations as of this morning.
(left) normalized by volume, (right) no volume normalization. The three blue curves show the dissipation of the global periodic solution in three boxes, [4pi, 8pi], [4pi, 16pi], and [4pi, 24pi]. Note that local curves lie on top of one another at the beginning of snaking on the right. They're actually the same localized solution embedded in laminar background flow of different sizes, so they have the same unnormalized dissipation.
I don't expect to get a lot done on this this week. I have some other things I have to get done, a deadline for a paper review, edit proofs for our most recent JFM paper, must make some progress on computing on Poincare sections, plus a drugged-up hour in the dentist's chair tomorrow. ![]() . The continuations will keep chugging away. I also have the eigenvalues computed along the [4pi, 16pi] curve but have not addressed the bookkeeping problem. Probably will address on saddle-node by hand and then try to automate the sorting.
. The continuations will keep chugging away. I also have the eigenvalues computed along the [4pi, 16pi] curve but have not addressed the bookkeeping problem. Probably will address on saddle-node by hand and then try to automate the sorting.
2009-07-28
Good news: I found the bug in my code that prevented computation of traveling-waves. As expected, it was a single-character typo, an ax in place of an az in one spot in my C++ implementation of the plane Couette symmetry group. It doesn't harm any previous work, just prevented progress on traveling waves. (Note that our most recent paper has many more eqbs than tws….). So I've started continuation of the localized traveling wave and have got it down from Re=400 to Re=190 overnight. It's clinging pretty close to the related EQB. Figures in a while.
I will probably have to shift computations to the Georgia Tech PACE cluster, now that the kinks are worked out and I have upwards of six to run at once. Disk space will be a problem. I need to keep parametrically continued solutions around and also their eigenfunctions. For [24pi, 2, 16pi] domains and 32 x 33 x 256 gridpoints, fields are about 3 MB each. That adds up fast towards my 11 GB limit on PACE, esp since I'm starting at about 10 GB full already. I need to figure out a way to back up that 10 GB over the internets to my home machine and then delete it to have some fresh workign space. That or get more disk on PACE.
 PC 2009-07-28: I think I reported this to John in April, but just in case I did not - When I visited Yohann Duguet duguet@mech.kth.se on his birthday Apr 21, 2009, he showed me their localized equilibria in very large aspect ratio pCf. As he wrote to me before my Stockholm visit “I have been busy on Steady States and other things in large domains for pCf and some pipe.” As they have a supercomputer, his aspect ration was large, let's say a few hundred (do not remember the number). Looked like some of your stuff, but that would need to be compared in detail. They did not do continuations and detailed studies of bifurcations like you do.
PC 2009-07-28: I think I reported this to John in April, but just in case I did not - When I visited Yohann Duguet duguet@mech.kth.se on his birthday Apr 21, 2009, he showed me their localized equilibria in very large aspect ratio pCf. As he wrote to me before my Stockholm visit “I have been busy on Steady States and other things in large domains for pCf and some pipe.” As they have a supercomputer, his aspect ration was large, let's say a few hundred (do not remember the number). Looked like some of your stuff, but that would need to be compared in detail. They did not do continuations and detailed studies of bifurcations like you do.
They had some difficulties in making the solutions converge. The problem is the usual heteroclinic problem - from laminar at far left to localized shadow of a state close to ones computed on spatially periodic domains, and then again heteroclinic to the laminar. My suggestion was as usual - use analytic information from the linearization of heteroclinic equilibria to patch from left infinity to someplace close to the solitary stationary state, same on the right side. Have not talked to him since, so do not know what they have done more recently.
![]() I remember you mentioned Yohann's work on this, but I did not contact him as Tobias wants to keep this between us until we publish a first paper. Our spatial domains are Lx=4pi, Ly=2pi, and Lz=8pi, 16pi, 24pi, and a bit of work so far at 32pi, so our aspect ratios go up to about 50:1 in x. Grid sizes are 32 x 33 x 128, 256, 384, or 512. We don't have any trouble with solutions not converging. By solving for the x,y,z variations simultaneously, we are in a sense computing the heteroclinic orbit you mention variationally. i.e the time-like variable is discretized like space and we find solve for the whole loop at once. Right now we don't know anything about the spatial instabilities of the laminar flow, but that could be addressed. Come to think of it, that's what the recent Marsden paper was about. JFG 2009-07-29
I remember you mentioned Yohann's work on this, but I did not contact him as Tobias wants to keep this between us until we publish a first paper. Our spatial domains are Lx=4pi, Ly=2pi, and Lz=8pi, 16pi, 24pi, and a bit of work so far at 32pi, so our aspect ratios go up to about 50:1 in x. Grid sizes are 32 x 33 x 128, 256, 384, or 512. We don't have any trouble with solutions not converging. By solving for the x,y,z variations simultaneously, we are in a sense computing the heteroclinic orbit you mention variationally. i.e the time-like variable is discretized like space and we find solve for the whole loop at once. Right now we don't know anything about the spatial instabilities of the laminar flow, but that could be addressed. Come to think of it, that's what the recent Marsden paper was about. JFG 2009-07-29
 PC 2009-07-30: Tobias hopefully believes in actually writing up papers. I will feel like I have really joined the ranks of fluid dynamicists (as the scientific ethics goes) if the first Yohann hears about “Atlanta” group spatially localized work is by checking contents of J Fluid Mechanics, so please tell him about your work when your draft is written up, and cite him as is a custom among colleagues.
PC 2009-07-30: Tobias hopefully believes in actually writing up papers. I will feel like I have really joined the ranks of fluid dynamicists (as the scientific ethics goes) if the first Yohann hears about “Atlanta” group spatially localized work is by checking contents of J Fluid Mechanics, so please tell him about your work when your draft is written up, and cite him as is a custom among colleagues.
 PC 2009-07-30: On spatially localized solutions, dynamical systems angle
PC 2009-07-30: On spatially localized solutions, dynamical systems angle
TMS 2009-07-30: Just to briefly clarify: Yohann of course knows about the first observations of those localized structures as we (mostly Bruno) have been talking about Daniel's and my work for more than a year on conferences - this is where the whole story started. The only problem is (and we (meaning the Marburg group) are responsible for that) is that these results still have not been written up - personally I believe in actually writing papers but there are sometimes 'other constraints' slowing things down. I just don't want to further increase chances that somebody publishes these results first by spreading the news that we have even identified the mechanism by which they are generated - that's all.
Here is an example of one of the talks - you'll even find plots of the states online:
http://www.newton.ac.uk/programmes/HRT/seminars/090909401.html
Dan Henningson was there speaking at the same day as were John and Predrag. Yohann was speaking at the next day - of course he knows about that.
 PC 2009-07-30: feeling better, thanks - one of these localized solutions is in Bruno's talk. I cannot remember whether Yohann's were localized both spanwise and streamwise. Will find out in Marburg in September.
PC 2009-07-30: feeling better, thanks - one of these localized solutions is in Bruno's talk. I cannot remember whether Yohann's were localized both spanwise and streamwise. Will find out in Marburg in September.
2009-07-29
Continuation of localized traveling waves. Found and fixed the bug that was preventing convergence of traveling-wave solutions, and so now I've got continuations of the localized traveling waves running. I've continued the [4pi, 8pi] localized traveling wave from Daniel Marinc's Re=400 down to its bifurcation point. Interestingly, it seems to be a secondary bifurcation off the localized eqb around Re=161, after the localized eqb bifurcates off the periodic solution around Re=150.2. That would explain why Daniel connected it to the periodic solution at the same Re as the eqb.
Continuation of a [4pi, 16pi]] TW is also running. I spliced 8pi worth of laminar flow onto the [4pi, 8pi] solution around Re=200 for an initial guess. This will probably show us the even/odd snaking behavior in conjunction with the [4pi, 16pi] eqb. Right now it is just getting started up the ladder.
The midplane of the localized TW and EQB on [4pi, 16pi] at similar parameter values. TW is (Re,D) = (174.78, 1.301); EQB is (Re, D) = (174.60, 1.324). The 'even'/ 'odd' symmetries of the TW / EQB are
 &= [u,v,-w](x+L_x/2, y, -z) \;\;\; \text{'even' TW symm} \\
[u,v,w](x,y,z) &= [-u,-v,-w](-x,-y,-z) \;\;\;\; \text{'odd' EQB symm}
\end{align*} $](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img0dbccdf61b1322bcc3b06371cc2e66da.png)
I've verified that these are the correct symmetries numerically. I think there must also be spanwise-traveling solutions with symmetry [u,v,w](x,y,z) = [-u,-v,w](-x,-y,z).
2009-08-01
Continuation with the 'even' traveling wave and real part of leading eigenvalues at lowest-D' saddle-node bifurcation of 4pi,16pi localized equilibria, at about (Re, D') = (171.73, 0.7). The localized eqb is produced in a saddle-node bifurcation in Re, with the second leading eigenvalue (red) crossing the real axis at the bifurcation point. The eigenvalues shown are all real, except the magenta lines and the portion of the red line after it joins with the blue. These are each complex pairs.
TMS: Great! Thus, as a function of the arclength the saddle-node bifurcation is the crossing of the red ev. Soon after that bifurcation also the green ev crosses the axis - might that be the symmetry-breaking bifurcation that gives rise to the 'ladders' connecting the 'even' and 'odd' snake?
The bifurcation diagram is great - both snakes wind around each other exactly as expected.
JFG: Yep! ![]() I don't that green ev crossing has anything to do with the even/TW solution solution. The symmetry of the TWs and EQBs are distinct (see previous entry); the eigenfunctions of the EQBs are going to be symmetric or antisymmetric in the EQB symmetry, which would lead to new solutions with either the same symmetry or no symmetry, but not the different symmetry of the TWs. The TWs and EQBs just above Re=150.2 in the 4pi.8pi case. I will have to examine the EQB eigenvalues there to understand how the TW breaks off from it. Maybe the EQB has both the 'even' and 'odd' symmetries listed above until that bifurcation pt.
I don't that green ev crossing has anything to do with the even/TW solution solution. The symmetry of the TWs and EQBs are distinct (see previous entry); the eigenfunctions of the EQBs are going to be symmetric or antisymmetric in the EQB symmetry, which would lead to new solutions with either the same symmetry or no symmetry, but not the different symmetry of the TWs. The TWs and EQBs just above Re=150.2 in the 4pi.8pi case. I will have to examine the EQB eigenvalues there to understand how the TW breaks off from it. Maybe the EQB has both the 'even' and 'odd' symmetries listed above until that bifurcation pt.
TMS: That is perfectly fine. I understand that both symmetries ('even' and 'odd') are distinct. The symmetry-breaking bifurcation only has to break the symmetry of the branch it bifurcates from - here the symmetry of the EQB. If it is a ladder it will than - after following it - reconnect to the TW branch. Thereby it connects the 'even' and 'odd' branch but does not show any symmetry itself. Nevertheless you should (for nummerical purposes) assume that the non-symmetric connection is not an EQB but a non-symetric TW because for physical reasons, breaking of the EQB-symmetry will most likely make the solution 'drift' downstream.
2009-08-07
Updated continuation plots. I've changed the colors to highlight the 4pi,16pi EQB and TW in red and blue. The TW has joined with the Nagata EQB at about (Re,D') = (131,1.5). The EQB continues upwards to about Re=300 without joining the Nagata solution; it has a defect. Perhaps as Re gets larger the wavelength gets more flexible and the EQB joins the periodic solution.
Below are the EQBs (left) and TWs (right) on 4pi,pi at the dots marked above, going up the snaking ladder. Note the value of D in the plot labels below is not the same as D' plotted above. Sorry, the bookkeeping requires me to stick with D in file label to keep my sanity.
2009-08-18
Aiming to look at symmetries of bifurcations of 4pi,8pi EQB and TW off globally periodic solution. This requires some preparatory work. These were my first localized continuations and I haven't aligned their spatial phases. I need to do that, with it in mind that they should bifurcate off the same phase in the globally periodic solution.
2009-08-20
Globally periodic Nagata solution
The periodic Nagata solution in a 4pi,8pi box at Re=140.4, shortly before bifurcation into localized solutions. This solution has an order-16 symmetry group with two generators a,b
s sx sy sz ax az factorization 1 1 1 1 0 0 e 1 1 1 -1 1/2 1/8 a 1 1 1 1 0 2/8 a^2 1 1 1 -1 1/2 3/8 a^3 1 1 1 1 0 4/8 a^4 1 1 1 -1 1/2 5/8 a^5 1 1 1 1 0 6/8 a^6 1 1 1 -1 1/2 7/8 a^7 1 -1 -1 -1 0 0 b 1 -1 -1 1 1/2 1/8 a b 1 -1 -1 -1 0 2/8 a^2 b 1 -1 -1 1 1/2 3/8 a^3 b 1 -1 -1 -1 0 4/8 a^4 b 1 -1 -1 1 1/2 5/8 a^5 b 1 -1 -1 -1 0 6/8 a^6 b 1 -1 -1 1 1/2 7/8 a^7 b
The symmetries are parameterized above as follows. If symmetry g = (s, sx, sy, sz, ax, az), then
g [u,v,w](x,y,z) = s [sx u, sy v, sz w](sx x + ax Lz, sy y, sz z + az Lz)
Localized EQB
The localized EQB at Re=156.66, shortly after bifurcation from the Nagata solution. After bifurcation at Re=150.2, this solution has single symmetry, a
1 -1 -1 -1 0 0
Localized TW
The localized EQB at Re=156.39, shortly after bifurcation from the Nagata solution. After bifurcation at Re=150.2, this solution has single symmetry, b
1 1 1 -1 1/2 1/8
Eigenfunctions at bifurcation
The real and imaginary parts of the eigenfunction of the complex eigenvalue that crosses the real axis ar Re=150.2 (here taken from a closeby datapoint Re=149.97). These eigenfunctions have a single antisymmetry
1 1 1 1 0 0.5
I don't understand how these eigenfunctions can produce the EQB and TW solutions above. Shouldn't they be symmetric under symmetries preserved through the bifurcation and antisymmetric under those broken? Is it possible to restore the desired symmetries by taking linear combinations of the real and imaginary parts?
2009-08-22
PC: An idea for alternative visualization of your spatially localized but wiggly solutions. In our Lan and Cvitanovic and Cvitanovic, Davidchack and Siminos Kuramoto-Sivashinsky papers we found it useful to use a visualization originally due to Michelson, of plotting the physical field u(x) vs. its spatial derivatives:

In visualization 5.1 (d) every periodic equilibrium and relative relative equilibrium is a loop - this could be especially convenient for visualization of your spatially localized but wiggly solutions, as the gradient vs gradient plot would be finite range in all directions, so you would not have to draw all these vertically narrow but horizontally repetitive wide plots. You have 3 fields (u,v,w), but as wiggliness is spanwise, something like plot of (w(x,y,z),∂_y v(x,y,z)) in a fixed x spanwise section, parametrized by 'time' y might be insightful. In the Kuramoto-Sivashinsky it guides the eye to “equilibria of equlibria” and the key role they play in imposing spatial periodicity on equilibria and traveling waves.
JFG: I agree that thinking about this with z as a timelike variable is something we need to do. But I think it needs some careful, maybe physics-based, thought on how to reduce the vastly greater number of dependent and independent variables, compared to KS. The idea of examining an independent variable and its derivatives as state-space variables I know through my work with Doyne Farmer and others in the 90s on state-space reconstruction. The KS case works well because you have a single unknown u and a single independent time variable x, and the dynamics can be expressed in terms of u and four x derivatives, so by plotting a few derivatives you are capturing almost everything about the dynamics. In the fluids case the much more drastic projection and effort involved makes me want to be careful about having a likelihood of success before investing effort. Like, the gentle variation in the x direction suggests projecting onto the first Fourier mode instead of taking a slice at one position in x. At the same time, such ideas are so POD-like that I am reluctant to start walking down that path. Basically i am saying I agree with the general motivation and direction of your post but think we need to stew on it a while longer before launching into computations.
2009-08-24
Some more information on the saddle-node bifurcation of the localized equilibrium, near the lowest red dot on the red 4pi,16pi EQB curve in the left figure above (from 2008-08-18). The two curves below show the eigenvalues of the 4pi,16pi EQB following upwards along the solution curve. Middle: Re λ vs Reynolds. Each color represents a single eigenvalue, tracked along the solution curve. The line style in the middle plot indicates the sides of the saddle node bifurcation: dotted is the lower-D branch, solid is the upper-D branch. Thus in the saddle-node bifurcation, the upper branch gets the stable eigenvalue (the solid blue line has Re λ < 0) and the lower branch gets the unstable eigenvalue (the dotted blue line has Re λ < 0). Note also that the eigenvalue shown in red passes through Re λ = 0 shortly after the saddle-node bifurcation. Perhaps this gives rise to rungs on the snaking ladder connecting the EQB and TW solutions. Right Im λ vs Re λ. I think it's harder to see the bifurcations in this plot or to see how're they're related to the snaking curve in D vs Reynolds plots. Below the EQB solution near the bifurcation point and the eigenfunction associated with the saddle-node bifurcation.
The EQB solution has the 16th-order symmetry group generated by
1 1 1 -1 0.5 0.125 1 -1 -1 -1 0 0
The eigenfunction has only the second of these two symmetries.
2009-09-08
JB I agree that the localized EQB solution has the second of the two symmetries listed above, but not the first. The globally periodic Nagata solution has both, but the first symmetry (which involves a shift in the spanwise z direction) is broken by the localized nature of the state. It is good that the eigenfunction with zero growth rate at the saddle-node shares the same symmetry as the underlying localized state. I expect the eigenfunction of the mode with zero growth rate slightly above the saddle-node (plotted in red) has a different symmetry.
JFG You're right. I was thinking of the globally periodic solution but that is not relevant here.
2009-09-29
Trying to answer some of the questions from our last meeting.
- Does snaking curve move left or right (lower or higher) in Re if Lx is increased? Answer: left
- Can we connect the EQ and TW solutions with a snaking ladder, by perturbing along the marginal eigenfunction that occurs shortly after the saddle-node bifurcation? Answer: So far, no.
- At fixed x, does the TW or EQ 'pump' fluid in the spanwise direction? y averaged or in yz plane?
Q1 I continued the 4pi,16pi EQ solution in Lx up to 4.08pi,16pi (nothing special about that value, just what I managed to get to overnight) and then continued that a bit in Re,D up and down the snaking curve. A short segment is shown in green on the snaking plot below. I believe we were hoping for the curve to go up, not down, so that we could argue that the local solutions in more realistic (larger) boxes might be important for transition, which happens around Re=350. But I'm not phased by finding the opposite. Just because a small perturbation of the solution we have our hands on goes the wrong way doesn't mean that at a much different Lx a more appropriate and possibly disconnected solution might appear. Do we know much about transition in this particular box, or in the box in which this state was found via an edge-state search?
Q2. I have initiated a number of searches for x-traveling waves on guesses of the form u = u0 + eps ef, where u0 is the EQB solution near the bifurcation point for the red eigenvalue shown in 2009-08-24 and ef is the corresponding eigenvalue. Free parameters are Re, eps, and wavespeed. I've tried a few different guesses with some manual tinkering to find local minima of the initial residual |u - sigma f^T(u)|, but so far my handful of searches have either converged back to u0 or failed to converge.
Q3. Haven't made such plots yet.
TMS: refering Q1: I have some runs for the 4pi x 16 pi box (turbulence decay studies) which show the existence of sustained non-laminar and temporally varying dynamics at Re = 240. But we haven't analysed this data yet and I don't know if there is anything yet published on the influence of the domain size. However the general trend seems to indicate, that wide but short boxes show `turbulence' at lower Re whereas long but narrow channels show higher `critical' Re. My suggestion for the paper than would be not to talk too much about the implications for the turbulence transition in the conclusions.
2009-10-02
Continuation of localized equilibrium in Lx, starting at Lx,Lz = 4pi,16pi and Re,D = 173.253,1.417. It appears that changing Lx does not produces a snaking curve in Lx,D. I expect that we we plot a number of different Lx-value snaking curves in Re,D, they would wobble back and forth around some central snaking curve.
The upper intersection of the curve with 4pi is the same point as the next upper intersection with Re=173.253 under Re continuation. The continuations are still running, will report with more data over the next few days.
2009-10-05 Update of above curve, continuation in Lx of localized EQB at fixed Re=173.253. A new snaking curve appears to be starting around Lx=17. The obvious question is “does this curve get wider or narrower as Re increases?” Presumably the flat tail of the D,Re continuations as Re gets large corresponds to the flat middle of this curve, so I'd guess that the curve gets wider as Re increases. So we might be able to find snaking of localized solutions at arbitrary large Re by pushing Lx downwards (upwards) until reaches pinning regions like the left and right of this curve. It is probably worth trying that at a few higher values of Re, say just above the present value, at Re=200, and Re=400. But probably not for the PRL –as always, trying any little thing opens up a new sets of other things to try, and one has to call a stop to it in order to get a paper out the door!
2009-10-06 Another update. What the heck is happening on the right, near Lx=17? The detail on the right shows a small loop. Will it continue in an upward snaking curve or continue drifting to the right, to larger and larger Lx? Meanwhile I am have taken the EQB solution at 5pi,16pi and am continuing it up and down in Re. Also writing some Python code to shift through my data files and directories to produce wavespeed vs Re curves.
Wavespeed
2009-10-06 Here's the wavespeed of the traveling-wave solution as a function of Re and of D. The wavespeed is in units of box length and time, in outer units, e.g. u(x,y,z,t) = f(x - cx t, y,z).
Pumping
2009-10-07 In a nutshell, in xz-average the EQB pumps fluid left (-z) near the bottom wall and right (+z) near the top, which is consistent with its [u,v,w](x,y,z) = [-u,-v,-w](-x,-y,-z) symmetry (that is, xz-avg w(y) is odd). The TW's z-reflection symmetry [u,v,w](x,y,z) = [u,v,-w](x+Lx/2,y,-z) requires that in xz-average w(y) = -w(y) = 0. On the other hand, the EQB symmetries require that the mean u on any yz plane is zero, whereas TWs can have non-zero flux through yz planes.
(a) Spanwise velocity w(y), averaged over x and z, as a function of wallnormal distance y. The TW has zero xz-avg w(y) because this solution has a mirror symmetry in z, [u,v,w](x,y,z) = [u,v,-w](x+Lx/2, v, -z). The EQB has a rotation about the origin symmetry, [u,v,w](x,y,z) = [-u,-v,-w](-x,-y,-z), which allows for the xz-avg w(y) function to be odd, as shown above.
(b-e) Plots of x averages in yz plane, y vertical, z horizontal, with y expanded by factor of 3 for visibility. Left (b,d) EQB, right (c,e) TW. Top plots (b,c) show x-avg u(y,z) color-coded and x-avg [v,w](y,z) with arrows. Bottom plots (d,e) show x-avg spanwise velocity w(y,z) colorcoded, red positive and blue negative. Note that the EQB is (at least plausibly) predominantly red on top and blue on bottom, indicating net transport of fluid rightward in the upper half and leftward in the bottom. Figure (a) is the actual xz-average and shows the effect conclusively, albeit at a small magnitude (1e-04 relative to wall speed 1). The TW wave velocities are also about this small.
Breathing (not!)
I don't find evidence of breathing in the localized solutions. The plot above, right, shows the energy field averaged over x,y as a function of z, for the difference from laminar of the localized EQB solution at the three points marked b,k, and c in the left plot. The wavelength in the interior is close to constant, especially between k and b, which are wider and therefore have smaller edge effects creeping into the interior. The width of the bands near the edges appears to increase as you go up the snaking curve. I also checked a point halfway between k and b, and its energy plot falls right between that of b and k on the right, again indicating near-constant interior wavelength (with a slight monotonic increase) and monotonically increasing wavelength on the edges, as you go up the snaking curve.
I believe I have answered all the outstanding questions for the PRL. Whew!
5pi,16pi solution
2009-10-14 The continuation of the solutions in Re at 5pi,16pi does not follow the clear snaking pattern of seen at 4pi,16pi. The plot above shows the 5pi,16pi equilibrium (green), obtained by continuing in Lx to 5pi at around Re=200 then continued down in Re. That produces the lower of the two 5pi,16pi branches. The solution appears to start snaking but then undergoes a couple loops in the D,Re plane and then starts heading back twoards higher Re and lower D. The detail on the right shows the loop and a check of the green curve recomputed at higher spatial and temporal resolution.
The 5pi,16pi equilibrium at Re=170, upper and lower branches. Apparently somewhere in the loops show above right a defect is introduced in the center of the solution. The center of the solution has a sharper conflict between the high and low speed streaks that resembles several of the spatially periodic equilibrium solutions we found previously.
Eigenvalue count along 4pi,16pi EQ
Number of positive eigenvalues along the 4pi,16pi EQB solution, estimated with Arnoldi iteration. I say estimated for a few reasons
- The eigenvalues are resolved to single precision at best.
- There are two marginal (zero) eigenvalues associated with the x and z translation symmetries, which hover around zero (O(1e-08)) in numerical calculations but with unpredictable sign.
- It's harder for the Arnoldi iteration algorithm to resolve the near-marginal eigenvalues in the presence of the truly marginal translational eigenvalues.
- It's then hard to pinpoint exactly where a non-translational eigenvalue crosses zero, unless you sort the eigenvalues and eigenfunctions according to their symmetries and then track them individually along the curve.
- So the count reported above is merely a count of the numerical eigenvalues above a threshold of 1e-04, for the given point on the continuation curve.
- Counting positive versus negative eigenvalues can miss zero crossings if two eigenvalues cross zero in opposite directions between data points.
- The eigenvalues were calculated at finite intervals along the curve (small dots). The bigger solid circles mark data points at which a new number of positive eigenvalues was found, compared to the previous, as you go up along the curve. The actual point of the zero crossing should be between the solid circle and the previous small dot.
Ah, numerics…