Table of Contents
State space of HKW cell
Basis sets
2008-12-30 through 2009-01-06
I have been dissatisfied for quite a while with the projection basis sets I've used for plotting periodic orbits in the HKW cell. We don't have good equilibria there, so we can't easily do the translational-basis set we used for the narrow cell in the JFM08 paper. I have previously used a POD basis from the data of a single periodic orbit (P87p89). The plots were good, in that they showed turbulent trajectories lying in the same regions of state space as the periodic orbits, and forming similar pretty-well-defined shapes in whatever projection we looked at. But Predrag never liked this since it involved POD and averages, and to me, it was rhetorically weak to use a basis based on periodic orbits to argue that the periodic orbits live where turbulence is.
So, I decided to compare the orbit-POD basis to a translational basis based on a single velocity field (for Predrag) and a turbulent-data POD basis (for me). It turns out they're all remarkably similar.
Some key points:
- All results here are confined to the S-invariant subspace as defined in our JFM08 paper.
- Unlike the narrower γ=1.5 cell, in the HKW γ=1.67 cell, the streamwise phase of the roll/streak system never changes, at least in my observation. If the high-speed (red) streak starts in the middle of the box, it stays in the middle of the box, for thousands of time units.
- Thus, unlike the narrow cell, a translational basis need not include spanwise (z) half-cell shifts in order to (roughly) span the region of state space that a turbulent trajectory explores. That gives just a two-d basis:
 .
. - Since we don't have a good equilibrium to form a translational basis, I used the mean of the P87p89 orbit plus its half-cell shift in x (pictured below). In the figures these basis elements are labeled
e0 P87meantransande1 P87meantrans. - The turbulent POD basis was constructed from about two hundred samples over a trajectory of several thousand time units. The basis clearly reflects the fixed z-phase of the roll-streak structures.
- The POD basis sets were calculated without removing the mean first, and the mean is far from the origin, so the first (zeroth) POD mode corresponds to the mean of the data. This facilitated comparison with the translational basis.
- The POD calculations also explicitly enforced symmetry under half-cell x translations. E.g. the averages were computed over both P87p9 and
 P87p89, and similarly for the samples of the the turbulent trajectory.
P87p89, and similarly for the samples of the the turbulent trajectory.
The mean of the P87p89 orbit and its half-cell shift in x,  , with and without the laminar flow.
, with and without the laminar flow.
Four basis sets
- en POD : POD of a turbulent trajectory and its
 symmetric partner.
symmetric partner. - en SSP : ON basis constructed from streak, roll and the Re and Im parts of the complex instability of roll+streak
- en P87p89 POD : POD of P87p89 and its
 symmetric partner.
symmetric partner. - en P87p89meantrans:

Main things to note:
The basis sets are very similar. That means that P87.89 explores the same region of state space as turbulence, in the crude let's-pretend-everything-is-a-Gaussian sense of the POD. Still, that is something, beyond the 1d plots showing that some orbits capture the mean and the Reynolds stresses within a few percent. Those 1d plots are averaged over x and z as well as time. Here we preserve the symmetry that breaks x,z homogeneity and find that the 3d average and multidimensional variances are very similar.
(Correction, 2009-01-05: The P87 POD basis elements shown above are corrected since the original posting. I think I had mistakenly copied the turbulent POD basis elements. The correspondence between the two sets is weaker but still strong. Note that the POD modes are ordered differently between the turbulent POD and the P87. E.g. turbulent POD mode e4 matches P87 POD mode e3. The sets are ordered by the variances of the imaginary Gaussian.)
It is not surprising that the translational basis based on the P87p89 mean is close to the P87p89 POD basis. The means of the P87p89 and  P87p89 orbit are far from the origin and relatively close together. Therefor it is not surprising that the first two POD modes of the full orbit are close to
P87p89 orbit are far from the origin and relatively close together. Therefor it is not surprising that the first two POD modes of the full orbit are close to  of the means of the two orbits.
of the means of the two orbits.
The P87p89 POD basis, however, continues on to e0, e1, e2, e3, … whereas the translational basis is just 2d. And the P87p89 POD basis is well-defined and easy to compute compared to the turbulent POD, because it is closed.
Note that for the POD bases, e0 and e2 have the same signs in the streaks but opposite signs in the rolls. That's in line with Wally's contention that the rolls and streaks are dynamically independent. Linear superposition of e0 and e2 can produce roll-streak combinations with different relative strengths of rolls and streaks. That such a superposition is present in the very lowest POD says that such variations in relative roll-streak strength happen frequently in the periodic orbit and turbulent flow.
Next thing is to compute state-space portraits of the orbits and turbulence for the periodic orbit paper. Also, it would be good to compare the e2 POD modes to the linear instability of the streaks a la self-sustaining process.
Addition 2009-01-06: SSP basis I added a column showing an SSP basis that I computed last spring following Waleffe Phys Fluids vol 9 no 4, 1997 closely (same cell size, frozen roll strength V=0.02). Main thing to note here is that the complex instability modes of the SSP basis are very similar to two of the POD modes. I.e., the POD modes arise from the complex instability from Wally's SSP.
e0 and e1 are given by

where “roll” is a [v,w](y,z) eigenfunction of the Stokes operator and “streak” is the asymptotic forced response u(y,z) to a frozen of strength V=0.02 (Wally's terminology, means maximum amplitude of v(y,z) = 0.02). c00 and c11 are determined by the choosing relative strengths of streaks and rolls to match means of DNS data and then normalizing to 1 (i.e. to match e0 of the POD basis sets). The coefficients for e1 are set by orthogonality to e0 and normalization.
e2 and e3 are computed this way: Compute the complex instability of frozen streak+roll in strengths comparable to DNS data. Orthogonalize to get e2, e3. There is an arbitrary choice of phase
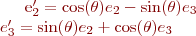
Chose  to maximize
to maximize  i.e. to best align
e2' and e3' with the e1 and e3 basis elements of the turbulent POD, respectively.
i.e. to best align
e2' and e3' with the e1 and e3 basis elements of the turbulent POD, respectively.
I know this probably sounds like an arbitrary concoction, but it does establish something new and important, I think: that those periodic orbits and the turbulent flow really are strongly associated with the complex instability of frozen streak+roll structures.

































