This labs shows how to do computer simulations of some basic physics, specifically, the flight of a baseball hit from home plate. We'll model the forces on the flying ball, including gravity and air resistance to produce the Newtonian equations of motion for the baseball in flight. The solution to these equations is the path of the baseball through the air.

Unfortunately, the equations of motion are too complicated to find an explicit formula for the solution using pencil and paper mathematics! So we'll use computer simulation techniques to approximate the solution numerically. We'll graph the path of the ball to see if it clears the outfield fence. Then we'll adjust the speed and angle of the ball off the bat to try to determine the minimum speed and optimal angle to hit a home run.

After that, we'll adjust the air density parameter to explore the difference between hitting a home run at Fenway and hitting one at Mile High Stadium in Denver.

The equations of motion for a baseball in flight with no air resistance are

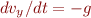
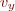Here and are the horizontal and vertical distances from home plate, and are the components of velocity in the and directions, and is the acceleration due to gravity. 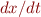means the rate of change of , and 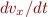means the rate of change of the velocity.

Note that these equations relate the rates of change of a set of variables to the values of those variables. This kind of system is called an Ordinary Differential Equation, or ODE.

We'll now implement some Matlab code to solve these equations numerically. We write a function f_nodrag in file fnodrag.m which defines the above equations of motion as a function mapping into .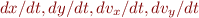

function dudt = f_nodrag(t, u) 
% equations of motion for baseball in flight without air resistance
 
    g = 9.8;    % acceleration of gravity m/s^2
 
    % extract components of vector u into variables x, y, vx, vy
    x  = u(1);
    y  = u(2);
    vx = u(3);
    vy = u(4);
 
    % compute rates of change of those components
    dxdt = vx;
    dydt = vy;
    dvxdt = 0.0;
    dvydt = -g;
 
    % pack rates of change back into vector dudt, return value of function
    dudt = [dxdt; dydt; dvxdt; dvydt];
end

Matlab expects equations like this to be written in vector form. So we let be a vector of the positions and velocities and 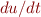be the vector of the rates of change of those quantities .

The equations of motion for a baseball in flight with turbulent air resistance are

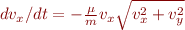
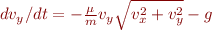
Here is a coefficient determined by the air density and the size of the baseball, is the mass of the baseball, and is the acceleration due to gravity. We encode those equations into the function f_withdrag as follows

function dudt = f_withdrag(t,u) 
% equations of motion for baseball in flight with turbulent air resistance
 
    rho_air  = 1.196;     % kg/m^3, density of dry air, 21 C, sea level   (Fenway)
    C = 0.3;              % drag coefficient for baseball (rough sphere)
    g = 9.81;             % acceleration due to gravity in m/s^2
    r = 0.0375;           % radius of baseball in m (3.75 cm)
    A = pi*r^2;           % cross-sectional area of baseball in m^2
    m = 0.145;            % mass of baseball in kg (145 gm)
    mu = rho_air*C_D*A/2; % coefficient of nonlinear |v|^2 term, in mks units
 
    % extract components of vector u into variables x, y, vx, vy
    x  = u(1);
    y  = u(2);
    vx = u(3);
    vy = u(4);
 
    % compute rates of change of those components
    dxdt = vx;
    dydt = vy;
    dvxdt = -mu/m * vx * sqrt(vx^2 + vy^2);
    dvydt = -mu/m * vy * sqrt(vx^2 + vy^2) - g;
 
    % pack rates of change back into vector dudt, return value of function 
    dudt = [dxdt; dydt; dvxdt; dvydt]
end

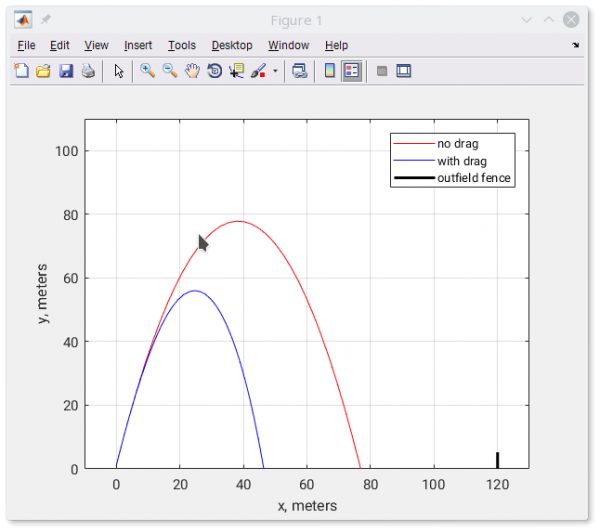
The file ``baseballsolve.m`` solves the above equations with some numerical solution methods, given the initial position and speed of the ball, and makes a plot that compares the flight of the ball with and without air resistance.

% Compute the trajectory of a baseball in flight, with and without 
% air resistance and plot results
 
x = 0.0;      % horizontal position of home plate, meters
y = 1.0;      % height of ball over strike zone
v = 40.0;     % initial speed of ball, meters per second
theta = 76;   % angle of ball off bat, degrees
 
% initial position and speed of ball
u0 = [x, y, v*cosd(theta), v*sind(theta)]; 
 
% solve for the first ten seconds of flight
tspan = [0 10];  
 
% solve the baseball equations numerically. ode45 is Matlab's numerical algorithm for ODEs
[t, u_withdrag] = ode45(@f_withdrag, tspan, u0);
[t, u_nodrag]   = ode45(@f_nodrag,   tspan, u0);
 
% get the x,y coordinates from the solutions and plot
figure(1); clf()
x = u_nodrag(:,1);
y = u_nodrag(:,2);
plot(x, y, 'r-')
hold on
 
x = u_withdrag(:,1);
y = u_withdrag(:,2);
plot(x, y, 'b-')
 
% plot outfield fence at x = 120 m (390 ft) and y = 0 to 5.2 m (17 ft)
plot([120, 120], [0, 5.2], 'k-', 'linewidth',2) 
 
legend('no drag', 'with drag', 'outfield fence')
 
grid on
xlim([-10, 130])
ylim([0, 110])
xlabel("x, meters")
ylabel("y, meters")
title("baseball trajectory")

You can run the Matlab code by typing ``baseballsolve`` at the Matlab prompt.

>> baseballsolve

A plot like this should appear

The thick black line shows the outfiled fence at 390 ft or 120 m, and 17 ft or 5.2 m high.

• How important is the effect of air resistance?

• Air density at Fenway park (sea level) is 1.196 kg/m^3. At one mile high in Denver, it's 0.986 kg/m^3. How much does the change in density affect the path of the ball at different angles and speeds? Try to change the above codes to show the path of the ball for both Fenway and Denver conditions. See if you can find a speed and angle that gives a home run in Denver but not at Fenway.

• Play around with the parameters in the functions, like the speed and angle of the ball. Can you figure out the minimum speed and optimal angle to just clear the outfiled fence and hit a home run?

Hitting a home run