gibson:teaching:spring-2018:math445:lecture:loglinear
Log-linear relations
Logarithmic plots are useful when the data you're plotting varies over many orders of magnitude. Logarithmic plots can also highlight certain functional relationships
| plot command | functional relationship |
|---|---|
plot(x,y) |  |
semilogy(x,y) | 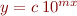 or or 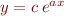 |
semilogx(x,y) |  |
loglog(x,y) | 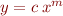 |
In lecture I will show (1) why each of these functional relationships appears as a straight line in the corresponding plot command and (2) how to estimate the values of the constants from a graph, in order to estimate  as an explicit function, given a few data points.
as an explicit function, given a few data points.
You can derive these formulae from the log-linear relations instead of memorizing them. For example, you can derive  by exponentiating both sides of
by exponentiating both sides of 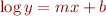 .
.
gibson/teaching/spring-2018/math445/lecture/loglinear.txt · Last modified: 2018/02/05 17:44 by gibson
