Table of Contents
Math 445 lab 8: 3d graphics
Important matlab commands:
linspace meshgrid pcolor surf surfc contour contourf quiver plot3 colorbar load subplot shading
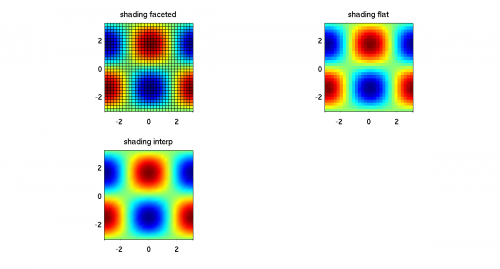
Problem 1: pcolor, meshgrid, shading, subplot
Skim the Matlab documentation for linspace, meshgrid, and pcolor. Create a 2D mesh from −π to π with 30 points in both the x and y directions. Then for each position in the mesh let z = cos(x) sin(y). Use pcolor, axis equal, and axis tight to generate this figure:

But don't you hate those ugly black lines? You can get rid of them with the shading command. Use subplot and the shading command to generate this figure:
Problem 2: surf
Create a 2D mesh from −π to π with 20 points in both the x and y directions, let z = cos(x) sin(y) pointwise, and then recreate this figure using the surf and colorbar commands.
Problem 3: surf in the shade
Create a 2D mesh from −10 to 10 with 100 points in both the x and y directions,
let 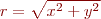 and
and z = 5 sin(r)/r. Then recreate Figure 4 using the surf and shading commands.
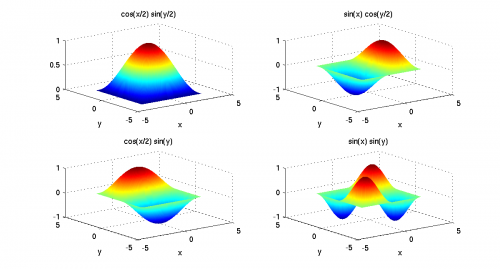
Problem 4: surf 'n' subplot
Create a 2D mesh from −π to π with 100 points in both the x and y directions and
then recreate Figure 5, using the functions z = cos(x/2) cos(y/2), z = sin(x) cos(y/2),
z = cos(x/2) sin(y), and z = sin(x) sin(y).
Problem 5: mystery plot
Enter the following code into a script file, save the figure produced as a '.jpg' or '.png' image, and include it with your project. What does the image produce? What is the role of the 'C' variable?
[phi,theta] = meshgrid(linspace(0,2*pi,100)); X=(cos(phi) + 3) .* cos(theta); Y=(cos(phi) + 3) .* sin(theta); Z=sin(phi); C=sin(3*theta); surf(X,Y,Z,C) shading interp
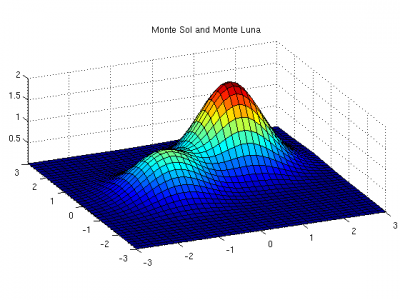
Problem 6: quiver plot
The function
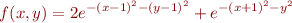
is a rough scale model of a pair of small mountains named Monte Sol and Monte Luna on the outskirts of Santa Fe, New Mexico. Monte Sol, the bigger of the two mountains is about 200 meters high above the plain, so the scale is 1 = 100 meters.
(a) Reproduce the above surface plot in Matlab.
(b) In a gentle rainstorm, water will flow down the mountains in the direction of steepest descent, i.e. along the negative of the gradient of  . Find the gradient of
. Find the gradient of  using elementary calculus, then make an
using elementary calculus, then make an  plot with both contours of the mountain height
plot with both contours of the mountain height  and a quiver plot showing the direction of flow of rainwater.
and a quiver plot showing the direction of flow of rainwater.
Problem 7: inviscid fluid flow within a square corner
The inviscid 2d fluid flow within a square corner with solid walls at  and
and  and the domain
and the domain  and
and  has velocity components
has velocity components
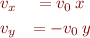
Make a quiver plot of this flow for  and
and  , and with
, and with  . Label the axes and title the plot.
. Label the axes and title the plot.
Problem 8: inviscid fluid flow past a semicircular bump
The inviscid 2d fluid flow past a semicircular bump of radius  centered at the origin on a flat wall at
centered at the origin on a flat wall at  has velocity components
has velocity components
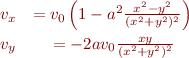
Make a quiver plot of this flow for  ,
,  ,
,  and
and 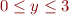 , excluding the interior of the bump, where
, excluding the interior of the bump, where 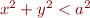 . Draw a blue curve that shows the surface of the semicircular bump. Make the
. Draw a blue curve that shows the surface of the semicircular bump. Make the  and
and  axis have the same scale, label the axes, and title the plot.
axis have the same scale, label the axes, and title the plot.
Bonus
Draw a Klein bottle in Matlab. Feel free to search the web, but understand whatever you use.
Attribution: Parts of this lab are adapted from Prof.Mark Lyon's Math 445 Advanced Graphics lab, which is adapted from Octave demos at http://yapso.sourceforge.net/demo/demo.html.