Math 445 lab 3: scripts, log-linear relations
Write a single Matlab script file that solves the following problems, and use the Matlab ''publish'' function to create a nice-looking PDF of your code and graphs to turn in. Be sure to label each problem with comments like %% Problem 1%% so that the problems are separated and labeled in the PDF.
Problem 1: Redo problem 15 from lab 2 using a Matlab script. The problem is make a plot of the polynomial 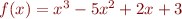 over the range
over the range  . Give the plot square axes and the title “math 445 lab 3 problem 1”.
. Give the plot square axes and the title “math 445 lab 3 problem 1”.
Problem 2: Make a plot of  over the range
over the range  using a dashed magenta line. Chose an appropriate plotting function that best displays the functional relationship between
using a dashed magenta line. Chose an appropriate plotting function that best displays the functional relationship between  and
and  . Label the axes and place a coordinate grid within the plot. Title the plot “math 445 lab 3 problem 2”.
. Label the axes and place a coordinate grid within the plot. Title the plot “math 445 lab 3 problem 2”.
Problem 3: Make a plot of 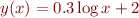 over the range
over the range  using a dot-dashed cyan line. Chose an appropriate plotting function that best displays the functional relationship between
using a dot-dashed cyan line. Chose an appropriate plotting function that best displays the functional relationship between  and
and  . For this plot, it's best to create the
. For this plot, it's best to create the x vector with logspace rather than linspace; e.g. x = logspace(0,5,20) will set x to 20 points between 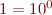 and
and 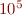 which are uniformly spaced on a logarithmic plot. Label the axes, set the
which are uniformly spaced on a logarithmic plot. Label the axes, set the  range of the plot to
range of the plot to 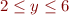 , and place a coordinate grid within the plot. Title the plot as in previous problems.
, and place a coordinate grid within the plot. Title the plot as in previous problems.
Problem 4: Make a plot of 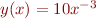 over the range
over the range 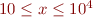 using a solid green line. Chose an appropriate plotting function that best displays the functional relationship between
using a solid green line. Chose an appropriate plotting function that best displays the functional relationship between  and
and  . Use the
. Use the logspace function for x as in problem 3. Label the axes, set the  range of the plot to
range of the plot to  , and place a coordinate grid within the plot. Title the plot as in previous problems.
, and place a coordinate grid within the plot. Title the plot as in previous problems.
Instructions for problems 5,6,7: For these problems you will deduce the functional relationship between variables in data sets using graphical analysis. The data sets are given as N x 2 matrices with x as the first column and y as the second. For each data set, you will find a function y(x) that fits the data, using the following steps:
- Download or cut & paste the data set to a text file with an appropriate name, e.g.
earthquake_magnitude.ascfor problem 1. - Load the dataset to Matlab with
load. For example,data = load('earthquake_magnitude.asc');. - Extract the two columns of the loaded data into two appropriately named vectors, e.g.
M = data(:,1);andN = data(:,2);will extract the M (magnitude) and N (number) columns of the earthquake-magnitude data matrix into vectorsMandNfor problem 5. For the remaining generic instructions I'll call these vectorsxandy. - Experiment with
plot,semilogy,semilogx, andloglogto determine the functional relationship betweenyandx. - Estimate the constants in the log-linear relationship graphically to determine the specific functional relation between
yandx. - Plot the estimated function and the data together, and fine-tune your function by adjusting the constants until there is a good fit between the estimated function and the data.
Once you have good fit between the data and the function, make a plot that shows
- the data set's y versus x as red circles
- your function y(x) as a solid blue line
- a legend indicating the meaning of each plotting symbol
- appropriate labels for each axis and a title
and provide an explicit formula for  .
.
Problem 5: The distribution of earthquake magnitudes, by Moment Magnitude scale. Big earthquakes are rare, and little earthquakes are frequent. In fact, there is a very clean empirical law that governs how many earthquakes of a given magnitude typically occur world-wide in a given year. Your job is to deduce that law from the following historical data.
- earthquake_magnitude.asc
% M N 8 2 7 18 6 120 5 800 4 6200 3 49000 2 365000 1 2920000
The first column is the moment magnitude M, and the second column is the number of earthquakes N of that magnitude that occur, on average, in a year. The last two entries are estimates, since it's impossible to detect every small earthquake around the world. The data are obtained from Earthquake Statistics and Earthquake Prediction Research by Stefan Wiemer, Institute of Geophysics, Zurich.
Using Matlab plotting commands, deduce the form of the functional relationship N(M). Estimate the constants in the relationship by estimating the slope and the y-intercept, and then fine-tuning by matching the plot of your estimate against the plot of the data. Your final answer should be an explicit formula for N(M).
Problem 6: The distribution of earthquake magnitudes, by energy. The moment magnitude scale is logarithmic, in that an earthquake of magnitude M+1 releases about 32 times more energy than an earthquake of magnitude M. The following dataset gives the number N of earthquakes in a given year of energy E measured in Joules.
- earthquake_energy.asc
% E N 6e16 2 2e15 18 6e13 120 2e12 800 6e10 6200 2e09 49000 6e07 365000 1e06 2920000
Deduce the form of the functional relation E(N) using Matlab plotting, then estimate and fine-tune the constants in the relation, and provide an explicit formula for E(N).
Problem 7: World population. The following data set provides the human population P of the earth at a given time t, measured in years A.D.
- world_population.asc
% t P 1927 2e09 1960 3e09 1974 4e09 1987 5e09 1999 6e09 2011 7e09
Deduce the form of the functional relation P(t), determine the constants graphically, and provide the explicit function P(t).
Assume that the formula you derived for P(t) is valid indefinitely into the future and the past. What year will the population of the earth reach one trillion? What year were the first humans born? Do you believe these answers? If not, why not?
