Think of the final exams as 2/3 (exam1 + exam2 + exam3 + systems of equations). That's about right to fit in the allotted two hours. There will be around eight problems chosen from this outline of topics.

• 1st order equations
  • separable
  • exact
  • 1st order linear
• 2nd and higher-order equations
  • homogeneous constant coefficient ( is your friend)
  • judicious guessing
  • variation of parameters
  • power series
• Laplace transforms
  • definitions, properties, and transforms & inverses of simple functions
  • s-translation, t-translation
  • Heaviside and Dirac delta functions
  • convolution
• Systems of equations
  • matrices, vectors, problems, and determinants
  • the eigenvalue problem, how it arises from the ODE
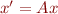
  • how to solve systems of ODEs with
    • real eigenvalues, distinct
    • real eigenvalues, repeated
    • complex eigenvalues (solutions expressed in both complex and real-valued forms)
  • phase portraits