Table of Contents
IAM 950 HW1
Problem 1
In class we derived via Taylor expansion the following approximation
for the exponential growth rate  of a sinusoidal perturbation of wavenumber
of a sinusoidal perturbation of wavenumber
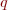 for a Type I-s instability, near the critical wavenumber (
for a Type I-s instability, near the critical wavenumber ( ), and close
to onset of instability (
), and close
to onset of instability ( ).
).
![LaTeX
\sigma_{q}(\epsilon) \approx \frac{1}{\tau_0} \left[ \epsilon - \xi_0^2 (q -q_c)^2 \right]](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgc195892edcfe4a614ae80a5b87fd9035.png)
Here  and
and  are system-dependent constants in units of time and length respectively.
are system-dependent constants in units of time and length respectively.
(a) Determine these constants for the 1d Swift-Hohenberg equation.
(b) Cross and Greenside describe  and
and  as characteristic time and length scales
of the instability. What observable characteristics of the Swift-Hohenberg equation do these time
and length scales govern?
as characteristic time and length scales
of the instability. What observable characteristics of the Swift-Hohenberg equation do these time
and length scales govern?
(c) Adapt the time-integration code for the Kuramoto-Sivashisky equation to Swift-Hohenberg, and use it to verify your answers to (b) with numerics.
Problem 2
Derive the reduced-order ODE model for the Swift-Hohenberg equation just above threshhold and at critical wavenumber and compare its behavior to numerical simulations of the PDE, in the following steps:
(a) Starting from the Swift-Hohenberg PDE on the periodic domain ![Math $[0, 2\pi]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img7806407f62e883177c7ca4d0d81c183c.png) and with
and with  ,
expand the unknown field
,
expand the unknown field  in Fourier modes
in Fourier modes

Substitute into the PDE, exploit orthogonality of the Fourier basis, and truncate to four modes  to obtain a system of four ODEs in the four coefficients (class notes 2012-02-08). You can fix the phase
to be even in
to obtain a system of four ODEs in the four coefficients (class notes 2012-02-08). You can fix the phase
to be even in  and use a cosine Fourier expansion, as we did in class, or use a complex Fourier basis
as written above to represent
and use a cosine Fourier expansion, as we did in class, or use a complex Fourier basis
as written above to represent  at arbitrary phase. In the latter case you will need to include the
complex conjugates of
at arbitrary phase. In the latter case you will need to include the
complex conjugates of  in the expansion.
in the expansion.
(b) Show that the equations for 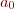 and
and  decouple, leaving a 2d system
of ODEs in just
decouple, leaving a 2d system
of ODEs in just 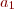 and
and  .
.
(c) Use Center Manifold Reduction to derive an algebraic model for  in terms of
in terms of 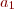 , and
then use that result to form a reduced-order nonlinear evolution equation for
, and
then use that result to form a reduced-order nonlinear evolution equation for 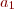 alone. What is the
long-term stable equilibrium state predicted by the reduced-order model?
alone. What is the
long-term stable equilibrium state predicted by the reduced-order model?
(d) Use a numerical ODE integration routine to integrate your ODE models from (b) and (c)
and the time-integration code from problem 1 for the PDE, for 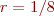 . For each model and the PDE simulation,
produce phase plots of
. For each model and the PDE simulation,
produce phase plots of  versus
versus 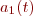 for a handful of initial conditions scattered in the
for a handful of initial conditions scattered in the
 plane. (If you used the complex Fourier representation, plot
plane. (If you used the complex Fourier representation, plot  versus
versus  and
choose real-valued initial conditions.) Plot the approximation of the center manifold on the phase plane
as well. You should see rapid approach to the center manifold followed by slow evolution on it.
and
choose real-valued initial conditions.) Plot the approximation of the center manifold on the phase plane
as well. You should see rapid approach to the center manifold followed by slow evolution on it.
(e) How accurate are the ODE models and the reduced-order equilibrium in the long term, as a function
of  ? Assume that the PDE simulation gives an accurate numerical solution of the Swift-Hohenberg
equation. Using the fixed initial condition
? Assume that the PDE simulation gives an accurate numerical solution of the Swift-Hohenberg
equation. Using the fixed initial condition  , produce a log-log plot
of asymptotic error
, produce a log-log plot
of asymptotic error

versus  where
where  is the asymptotic state of the PDE simulation and
is the asymptotic state of the PDE simulation and  is first the
the ODE model from (b), second the reduced-order model from (c), and third the reduced-order
equilibrium. Plot these as three lines in log-log plot of error versus
is first the
the ODE model from (b), second the reduced-order model from (c), and third the reduced-order
equilibrium. Plot these as three lines in log-log plot of error versus  . I suggest
using
. I suggest
using 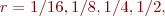 and
and  .
.
Note that the ODE systems for (b) and (c) will be stiff, in that the high-order coefficients evolve very rapidly until the system equilibrates to and moves slowly on the center manifold. You might need to use a stiff ODE integrator instead of the classic explicit schemes like RK4.
