Table of Contents
Quadrature
Quadrature is the numerical approximation of definite integrals of functions evaluated at discrete gridpoints.
There are many, many quadrature formulae. We will start with the Trapezoid Rule and Simpson's Rule.
In both cases we will assume we have an evenly spaced set of  gridpoints
gridpoints 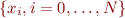 on the interval
on the interval ![Math $[a,b]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgfe477a2781d275b4481790690fccd15f.png) , with
, with 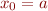 ,
,  , and
, and  , where
, where  is the gridspacing. We also assume we know the value of the function evaluated at the gridpoints, i.e. we have a vector of values
is the gridspacing. We also assume we know the value of the function evaluated at the gridpoints, i.e. we have a vector of values 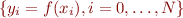 .
.
Trapezoid Rule
The Trapezoid rule approximates the definite integral of 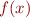 over
over ![Math $[a,b]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgfe477a2781d275b4481790690fccd15f.png) using piecewise linear
interpolation between each pair of datapoints.
using piecewise linear
interpolation between each pair of datapoints.
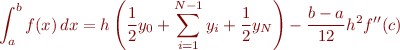
for some  where
where  .
.
For 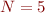 we would have
we would have
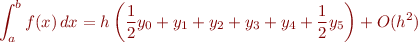
Here we have collapsed the error term into  .
.
Simpson's Rule
Simpson's Rule pproximates the definite integral of 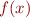 over
over ![Math $[a,b]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgfe477a2781d275b4481790690fccd15f.png) using piecewise quadratic
interpolation between triplets of datapoints.
using piecewise quadratic
interpolation between triplets of datapoints.
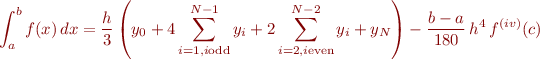
for some  where
where  , and where
, and where  is the fourth derivative of
is the fourth derivative of  . Simpson's rule requires that
. Simpson's rule requires that  is even, so that the total number of gridpoints,
is even, so that the total number of gridpoints,  , is odd.
, is odd.
For example, for 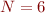 and
and  gridpoints, we have
gridpoints, we have

Further reading
- Trapezoidal rule (wikipedia)
- Trapezoidal rule (math world)
- Simpson's rule (wikipedia)
- Simpson's rule (math world)
- Newton-Cotes formulae (wikipedia)
- Newton-Cotes formulae (math world)
- Trapezoidal rule (math world)
