Math 753/853 QR and the least-squares problem
The QR decomposition is useful for solving the linear least-squares problem. Briefly, suppose you have an  system with an oblong matrix
system with an oblong matrix 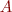 , i.e. A is an
, i.e. A is an  matrix with
matrix with  .
.
Each of the  rows of
rows of 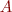 corresponds to a linear equation in the unknown
corresponds to a linear equation in the unknown  variables that are the components of
variables that are the components of  . But with
. But with  , that means we have more equations than unknowns. In general, a system with more equations than unknowns does not have a solution!
, that means we have more equations than unknowns. In general, a system with more equations than unknowns does not have a solution!
So, instead of looking for an  such that
such that  , we look for an
, we look for an  such that
such that  is small. Since
is small. Since  is a vector, we measure its size with a norm. That means we are looking for the
is a vector, we measure its size with a norm. That means we are looking for the  that minimizes
that minimizes 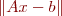 .
.
Let  . Thinking geometrically,
. Thinking geometrically,  will be smallest when
will be smallest when  is orthogonal to the span of the columns of
is orthogonal to the span of the columns of 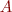 . Recall that for the QR factorization
. Recall that for the QR factorization 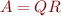 , the columns of
, the columns of  are an orthonormal basis for the span of the columns of
are an orthonormal basis for the span of the columns of 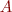 . So
. So  is orthogonal to the span of the columns of
is orthogonal to the span of the columns of 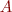 when
when
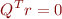
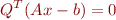
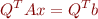
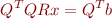
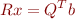
Since  is an
is an  matrix whose columns are orthonormal,
matrix whose columns are orthonormal, 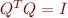 is the
is the  identity matrix. Since
identity matrix. Since 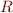 is
is  , we now have as the same number of equations as unknowns. The last line,
, we now have as the same number of equations as unknowns. The last line,  , is a square upper-triangular system which we can solve by backsubstitution.
, is a square upper-triangular system which we can solve by backsubstitution.
That's a quick recap of least-squares via QR. For more detail, see these lecture notes from the University of Utah.
