Lagrange Interpolating Polynomial
The Lagrange Interpolating Polynomial is a simple-to-understand but mathematically clunky way to construct an  -order polynomial interpolant to a set of
-order polynomial interpolant to a set of  data points
data points 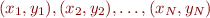 .
.
The best way to see it is by example for a quadratic fit to three data points 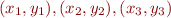 . Let
. Let 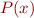 be
be
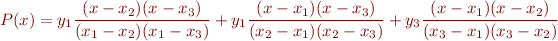
It's easy to see the polynomial goes through each data point. If you plug in  , the second and third terms vanish, and the fraction in the first term is
, the second and third terms vanish, and the fraction in the first term is 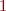 , so that
, so that 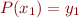 . Similar simplifications occur when plugging in
. Similar simplifications occur when plugging in 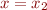 , to get
, to get 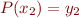 , and similar for
, and similar for 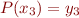 . Also, since everything on the right-hand-side except
. Also, since everything on the right-hand-side except  is a constant, it's clear that the
is a constant, it's clear that the 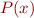 is a polynomial in
is a polynomial in  of order 2. The generalization to higher-order polynomials is straightforward.
of order 2. The generalization to higher-order polynomials is straightforward.
For example, let's fit a 2nd order polynomial to  . Plugging into the formula gives
. Plugging into the formula gives
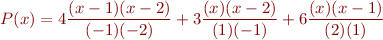
This is mathematically clunky because it expresses a quadratic polynomial 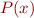 as the sum of three quadratics, and we have a lot of tedious algebra to do to simplify. If we do that, we get
as the sum of three quadratics, and we have a lot of tedious algebra to do to simplify. If we do that, we get
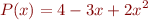
which can be easily verified as passing through the given data points.
Further reading
- Lagrange Interpolating Polynomial (Wolfram Mathworld)
- Lagrange Polynomial (Wikipedia)
