gibson:teaching:fall-2016:iam961:hw1
IAM 961 HW1
1. Prove that any linear map 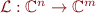 can
written as an
can
written as an  matrix. (Hint: let
matrix. (Hint: let 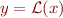 . Express
. Express  as a linear combination of the canonical basis vectors
as a linear combination of the canonical basis vectors 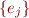 . Substitute that into
. Substitute that into 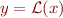 , then use linearity to rewrite the right-hand-side of this equation as a linear combination of vectors
, then use linearity to rewrite the right-hand-side of this equation as a linear combination of vectors 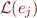 . Now take the inner product of both sides of this equation with
. Now take the inner product of both sides of this equation with  . That should give you
. That should give you  for some matrix
for some matrix  .)
.)
2. Prove that 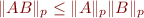 .
.
3. If  and
and  are
are  -vectors the matrix
-vectors the matrix  is known as a
rank-one perturbation of the indentity. Show that if
is known as a
rank-one perturbation of the indentity. Show that if 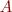 is nonsingular, then its inverse
has the form
is nonsingular, then its inverse
has the form 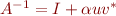 for some scalar
for some scalar  , and give an expression
for
, and give an expression
for  . For what
. For what  and
and  is
is 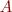 singular? If it is singular, what is
singular? If it is singular, what is 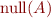 ?
(Trefethen exercise 2.6).
?
(Trefethen exercise 2.6).
gibson/teaching/fall-2016/iam961/hw1.txt · Last modified: 2016/09/07 08:56 by gibson
