Math 527 ungraded variation of parameters homework

problem 5 solution

(a) What property must an operator $L$ satisfy to be linear?

$\begin{eqnarray*} L (c_1 y_1 + c_2 y_2) = c_1 L y_1 + c_2 L_y_2 \end{eqnarray*}$

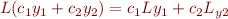
for all constants 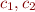$c_1, c_2$ and all functions $y_1(x), y_2(x)$ .

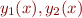(b) Why is linearity important for the solution of linear differential equations?

Because it allows you to express the general solution of the ODE as a sum of the other solutions.

(c) How many linearly independent solutions does an $n$ th order linear homogeneous equation have?

$n$

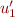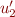(d) When you integrate $u_1'$ and $u_2'$ in variation of parameters, why can you always set the integration constant to zero?

Because 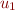$u_1$ and $u_2$ are coefficients of the homogeneous solutions $y_1$ and $y_2$ in the ansatz

$\begin{eqnarray*} y_p = u_1 y_1 + u_2 y_2 \end{eqnarray*}$

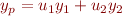
any constant included in the value of 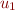$u_1$ or $u_2$ or could just be absorbed into the constants in front of $y_1$ and $y_2$ in the general solution. E.g.

$\begin{eqnarray*} c_1 y_1 + c_2 y_2 + y_p &= c_1 y_1 + c_2 y_2 + (u_1 + a) y_1 + (u_2 + b) y_2 \\ &= (c_1 + a) y_1 + (c_2 + a) y_2 + u_1 y_1 + u_2 y_2 \\ \end{eqnarray*}$

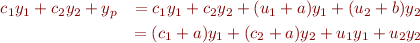
(e) What is Euler's formula?

$\begin{eqnarray*} e^{ix} = \cos x + i \sin x \end{eqnarray*}$

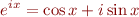
(f) How would you prove Euler's formula? Don't do the proof, just describe the proof in a sentence or two.

Substitute $ix$ in place of $x$ in the power series expansion of $e^x$ , then simplify and regroup so that the even terms become the power series for $\cos x$ and the odd terms become $i$ times the power series for $\sin x$ .

channelflow.org

User Tools

Site Tools

Math 527 ungraded variation of parameters homework

problem 5 solution

Page Tools