Math 445 mid-term exam with solutions

1. Write one line of Matlab code that returns the 4th column of the matrix 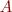$A$ .

A(:,4)

2. Write Matlab code that sets all entries in the 3rd row of the matrix 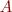$A$ to zero. Its possible to do this in one line, but you can use several.

A(3,:) = 0;

or

A(3,:) = zeros(1,size(A,2));

or

[M,N] = size(A);
A(3,:) = zeros(1,N);

3. Write one line of Matlab code for an anonymous function that computes the value of the polynomial $3x^2 - 2x - 7$ for an input argument $x$ .

f = @(x) 3*x^2 - 2*x - 7;

4. How would you use Matlab and the anonymous function from problem 3 to find a numerical solution to the equation $3x^2 - 2x - 7 = 0$ ? One line of code should do it.

x = newtonsearch(f,2);

or

x = fzero(f,2);

Note: 2 is an initial guess for the solution, chosen because f(2) = 1 (this is relatively close to zero).

5. Write one line of Matlab code that evaluates to 1 (true) if $x$ is negative and $y$ is positive, and 0 (false) otherwise.

x < 0 && y > 0

6. Write one line of Matlab code that evaluates to 1 (true) if both $x$ and $y$ are positive or if both are negative, and 0 (false) otherwise.

(x < 0 && y < 0) || (x > 0 && y > 0)

7. Write one line of Matlab code that counts how many components of the vector $v$ are exactly zero.

sum(v==0)

8. Show how to solve the system of equations with three lines of Matlab code.

$\begin{align*} 3x + y + 2z - 6 &= 0 \\ 9z - x - 8 &= 0 \\ 5y - 4x - 1 &= 0 \end{align*}$

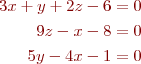
A = [ 3 1 2; -1 0 9; -4 5 0];
b = [6; 8; 1];
x = A\b

9. Write a Matlab function that computes the mean (i.e. average) of the components of a vector $x$ according to the formula

$\text{mean}(x) = (1/N) \sum_{i=1}^{N} x_i$

where $N$ is the length of the vector. Your function should evaluate this sum directly instead of using the Matlab sum or mean functions.

function m = mean(x)
% compute mean of vector x

  m = 0;
  N = length(x);
  
  for i=1:N
    m = m + x(i);
  end
  
  m = m/N;
end

10. Write a Matlab function that takes an $M \times M$ transition matrix $T$ for a network of $M$ web pages and returns the page rank vector $p$ of the steady-state distribution of visitors to each page. The page rank is given by $p = T^n e$ , where $e$ is an arbitrary $M$ -vector whose components sum to 1, and $n$ is large number. You can set $n$ to 100.

  
function p = pagerank(T);
% compute that page rank vector for transition matrix T

  [M,M] = size(T);

  e = zeros(M,1);
  e(1) = 1;
  
  n=100;
  
  p = T^n * e;
  
end

channelflow.org

User Tools

Site Tools

Math 445 mid-term exam with solutions

Page Tools