Table of Contents
Benchmarking a simple PDE solver in Julia and other languages
Julia
Julia is an innovative new programming language that promises to revolutionize scientific computing. In a nutshell, it is
- High-level, dynamic, and general-purpose, like Python
- As fast as compiled C, roughly
- Aimed squarely at numerics, with libraries and ease-of-use comparable to Matlab
Julia's main innovation is a carefully-designed type system combined with just-in-time compilation. The combination allows high-level user code to be compiled to machine-code on-the-fly.
The benchmark algorithm
The benchmark algorithm here is a simple time-integration of the Kuramoto-Sivashniksy equation

on a 1d periodic domain ![Math $[0, L_x]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img61b4afa6245877d9257087d6985d859f.png) , with
, with  space and
space and  time, and where subscripts indicate differentiation. The algorithm uses a Fourier decomposition in space and 2nd-order Crank-Nicolson, Adams-Bashforth semi-implicit finite-differencing in time, with collocation computation of the nonlinear term
time, and where subscripts indicate differentiation. The algorithm uses a Fourier decomposition in space and 2nd-order Crank-Nicolson, Adams-Bashforth semi-implicit finite-differencing in time, with collocation computation of the nonlinear term 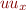 . I implemented the same algorithm in Python, Matlab, C++, and in two forms in Julia. The codes and a detailed description of the algorithm is given below.
. I implemented the same algorithm in Python, Matlab, C++, and in two forms in Julia. The codes and a detailed description of the algorithm is given below.
The results
The left plot shows execution time of 3200 time steps of the algorithm as a function of  , the number of gridpoints in the Fourier decomposition. The dominant cost of the algorithm should be the FFTs, which should scale as
, the number of gridpoints in the Fourier decomposition. The dominant cost of the algorithm should be the FFTs, which should scale as 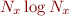 . All the codes use the same FFTW libraries, so ideally, they should all collapse onto the same
. All the codes use the same FFTW libraries, so ideally, they should all collapse onto the same 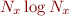 line as linear and fixed-size overheads costs decrease relative to that.
line as linear and fixed-size overheads costs decrease relative to that.
The right plot shows


