Math 445 lab 6: Google Page Rank
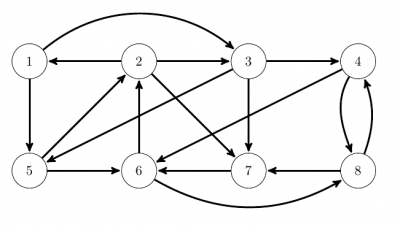
Problem 1: Hamster dynamics. Suppose you have 100 hamsters living in the following set of eight hamster houses connected by one-way tunnels.
Suppose that every minute at sound of a bell, each hamster runs down one of the tunnels in its present hamster house and appears in the house it connects to.
(a) Let  represent the fraction of hamsters in the
represent the fraction of hamsters in the  th house in the
th house in the  th minute. Write down a set of eight equations for
th minute. Write down a set of eight equations for  through
through  in terms of
in terms of  through
through  .
.
(b) Let  be the vector whose elements are
be the vector whose elements are  . Write the set of equations from (a) in terms of a matrix-vector multiplication,
. Write the set of equations from (a) in terms of a matrix-vector multiplication,  .
.
(c) Write Matlab code to compute the steady-state distribution of hamsters by computing  for some large value of
for some large value of  , say
, say 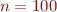 . For
. For  , start with either the same fraction of hamsters in each house or a random set of fractions that totals to 1.
, start with either the same fraction of hamsters in each house or a random set of fractions that totals to 1.
(d) Use Matlab's sort function to produce a list of the houses ranked in order of their steady-state populations.
Challenge: Revise your code show that uses Matlab's bar function to show a bar chart of the hamster distribution at each time step through the loop. Use Matlab's pause function to pause a short while on each step, so that you have time to see each bar chart.
Problem 2: Google Page Rank.
Compute the Google Page Rank for a network of 100 pages within www.unh.edu.
(a) Download the surfer.m Matlab script from Numerical Computing with Matlab by Clive Moler. Set M=100 and run the command [w,L] = surfer('http://www.unh.edu',M);. This might take a few minutes.
(b) After some time this will generate a vector  of websites and a matrix
of websites and a matrix  of links between them. All the entries of
of links between them. All the entries of  should be either 0 or 1. But
should be either 0 or 1. But  will have 100^2 == 10,000 entries, so you can't check this by eye. Write a short piece of Matlab code that double-checks that all entries of
will have 100^2 == 10,000 entries, so you can't check this by eye. Write a short piece of Matlab code that double-checks that all entries of  are either 0 or 1.
are either 0 or 1.
(c) Now from the matrix  , generate a transition matrix
, generate a transition matrix 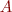 that governs the dynamics of people clicking on random links, according to
that governs the dynamics of people clicking on random links, according to  . Similar to the hamster dynamics problem above, the
. Similar to the hamster dynamics problem above, the  th component of the vector
th component of the vector  is the fraction of websurfers visiting the
is the fraction of websurfers visiting the  th webpage at time
th webpage at time  . You will probably run into problem, namely a webpage might contain no links or only links outside the set of pages we are working with. In that case we will just assume that the person randomly selects a new website among all the
. You will probably run into problem, namely a webpage might contain no links or only links outside the set of pages we are working with. In that case we will just assume that the person randomly selects a new website among all the  pages in our set. Revise your calculation of
pages in our set. Revise your calculation of 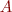 so that if a column of
so that if a column of  sums to zero, then each of the entries in the same column of
sums to zero, then each of the entries in the same column of 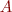 is
is 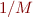 .
.
(d) Suppose that instead of always clicking on a random link within a page, a web surfer sometimes (with probability  ) jumps to a random page chosen from all the pages in the network. We can model this behavior by using a modified transition matrix
) jumps to a random page chosen from all the pages in the network. We can model this behavior by using a modified transition matrix  and dynamics
and dynamics  , as follows
, as follows
![Equation \begin{equation*}
B = (1-\alpha) A + \alpha [1]/M
\end{equation*}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img096a77a758b511927a3a1a1d72018c06.png)
where ![Math $[1]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgd478bbb960d11a0df52c338c436f402a.png) is an
is an  matrix of ones. Rumor has it that Google uses
matrix of ones. Rumor has it that Google uses 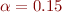 , so use that value and calculate
, so use that value and calculate  .
.
(e) Double-check that the sum of each column of  is 1. Again, be clever and get Matlab to do the work, rather than listing out the sums of all the columns and verifying manually that each of the 100 numbers is 1!
is 1. Again, be clever and get Matlab to do the work, rather than listing out the sums of all the columns and verifying manually that each of the 100 numbers is 1!
(f) Let’s assume that all websurfers start at the first webpage, p=zeros(M,1); p(1)=1;. If we applying B to p many times (say 40 times), the resulting vector will give the probability that we end up on a particular website and after a long session of random web surfing. We can do this with a for-loop
N=40; for n=1:N; p=B*p; end
After that is complete the elements of p give the probabilities that a random web surfer will end up at the web pages listed in w, and you can rank the pages in w according to their probabilities in p. Look up the sort command in the Help menu and find a way to print the list of websites in order of their rank. Turn in the list of the top 10, the fraction of the time a random web surfer would spend in each one of those 10, and your code to complete the Lab.
(g) If you are interested: Our calculation involved two free parameters: the probability  of jumping to an entirely random page in the network, and
of jumping to an entirely random page in the network, and  , the number that specifies the length of our long session of random web surfing. How robust is the page rank algorithm with respect to these two parameters? If you change
, the number that specifies the length of our long session of random web surfing. How robust is the page rank algorithm with respect to these two parameters? If you change  to 0.1 or 0.05, do the top 10 pages change?
How about if you change
to 0.1 or 0.05, do the top 10 pages change?
How about if you change M to 100 or 1,000?
Problem 3: Suppose that, instead of representing links between web pages, you have a directed graph that tells who likes whom among all students at UNH. You could then use the same algorithm to compute a numerical measure of each UNH student's likeability, and an overall ranking of the popularity of all UNH students.
What do you think of this proposal? Would the numerical values produced be meaningful measures of likeability or popularity? Why or why not? What does your answer here say about Google Page Rank as a method of ranking web pages?
Note: There is no single clear answer to this question. Just be thoughtful about it and express yourself clearly.