Math 445 exam 1 example questions
The exam will have around ten questions, some easy, some not so easy. For most questions, you will be asked to answer with Matlab code in correct syntax. E.g.
Problem 1: (totally straightforward) Given a matrix 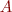 , write one line of Matlab code that would assign the 3rd row of
, write one line of Matlab code that would assign the 3rd row of 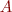 into the variable
into the variable  .
.
Problem 2: (slightly tricky) Given a matrix 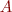 , write one line of Matlab code that convert the
, write one line of Matlab code that convert the  th column of
th column of 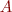 into a row vector and assign it to the variable
into a row vector and assign it to the variable  .
.
Problem 3: (pretty straightforward) Given a vector  , write one or two lines of Matlab code that would return all the odd-numbered elements of
, write one or two lines of Matlab code that would return all the odd-numbered elements of  . (By “odd-numbered elements”, I mean the elements with odd indices, e.g.
. (By “odd-numbered elements”, I mean the elements with odd indices, e.g. 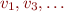 .)
.)
Problem 4: (moderate) Write Matlab code that defines a function named mysin that computes  using the truncated power series
using the truncated power series

Note: an earlier version of this problem had an error in the Taylor series of  .
.
Problem 5: (straightforward) Write Matlab code that would solve the system of equations.

Problem 6: (straightforward) Write a Matlab function that computes the mean (i.e. average) of
the components of a vector  according to the formula
according to the formula
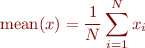
where  is the length of the vector. Your function should evaluate this
sum directly using a for loop, not by calling Matlab's sum or
mean function. You did this for lab, now see if you can do it without looking at notes.
is the length of the vector. Your function should evaluate this
sum directly using a for loop, not by calling Matlab's sum or
mean function. You did this for lab, now see if you can do it without looking at notes.
Problem 7: (straightforward) Write a few lines of Matlab code that would plot 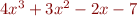 versus
versus  on the interval
on the interval  using a red dashed line. Label the axes.
using a red dashed line. Label the axes.
Problem 8: (a little harder than 7) Write a few lines of Matlab code that would plot 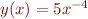 on the interval
on the interval  , using the plotting function that would best highlight the functional relation between
, using the plotting function that would best highlight the functional relation between  and
and  . Label the axes.
. Label the axes.
Problem 9: Deduce the functional relationship 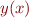 from this graph.
from this graph.

