Math 445 lab 4: dot syntax and plotting
Problem 1: Create a plot that shows 
and 
over 
with the sine in
green and the cosine in blue. Choose enough gridpoints that the curve looks smooth. Label the 
axis and
use a legend to label the curves.
Helpful Matlab commands: linspace, plot, xlabel, legend, help.
Problem 2: Consider the two functions 
and 
for the fixed value 
.
Which function increases faster as 
? (Hint: plot the two functions together
on the range 
, and plot the 
axis logarithmically.) Would the answer change
if you increased the value of 
?
Helpful Matlab commands: linspace, semilogy, xlabel, legend, help, plus dot-syntax.
Problem 3: How many real roots does the function 
have?
Determine this by plotting the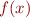 
and counting how many times it crosses zero.
Estimate the roots graphically to two digits by refining your plots in the neighborhood
of each zero crossing.
Helpful Matlab commands: linspace, plot, xlabel, ylabel, axis, plus dot-syntax. In
particular you can use axis([xmin xmax ymin ymax]) to zoom in on regions near zeros.
Or you can zoom in by refining the range of and replotting.
Problem 4: The exponential function 
can be computed from the power series
In practice one truncates the infinite sum to a finite number of terms, summing from 
to 
for
some fairly large 
. How large does need to be to calculate 
to sixteen digits? You can answer
this question very quickly by writing one line of Matlab code that evaluate the truncated sum for a fixed value of , and then rerunning it with changing values of .
Helpful Matlab commands: sum, format, exp (for getting the correct value of 
to sixteen digits), colon syntax, dot syntax, and log10 (for counting digits of precision).
Problem 5: The sine function can be computed from the power series
Like the exponential function, in practice one truncates this sum at . How large does need to
be to calculate 
to sixteen digits?
Helpful Matlab commands: same as problem 4.
