Polynomial Interpolation via Newton Divided Differences
Newton's Divided Difference algorithm is a slick way to compute an  th order polynomial interpolant to a set of
th order polynomial interpolant to a set of  data points
data points 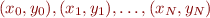 with distinct
with distinct  's.
's.
It produces a polynomial in the form of Horner's method with base points, e.g.
![Equation \begin{equation*}
y = P(x) = c_0 + (x - x_0) \, [c_1 + (x - x_1) [c_2 + (x - x_2) [c_3 + (x - x_3) \, c_4]]]
\end{equation*}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img4934d0556245ff1a549d820dc6d43675.png)
If we plug in the data points 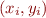 for
for 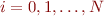 , to the
, to the  th-order generalization of the above equation, we get a series of
th-order generalization of the above equation, we get a series of  equations in the
equations in the  unknowns
unknowns 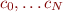 .
.
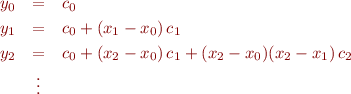
Lo and behold this is lower-triangular system of equations, which can be written in matrix form like this
![Equation \begin{equation*}
\left[\begin{array}{ccccc}
1 & & \ldots & & 0 \\
1 & x_1-x_0 & & & \\
1 & x_2-x_0 & (x_2-x_0)(x_2-x_1) & & \vdots \\
\vdots & \vdots & & \ddots & \\
1 & x_k-x_0 & \ldots & \ldots & \prod_{j=0}^{N-1}(x_N - x_j)
\end{array}\right]
\left[\begin{array}{c} c_0 \\ c_1 \\ c_2 \\ \vdots \\ \\ c_{N} \end{array}\right] =
\left[\begin{array}{c} y_0 \\ y_1 \\ y_2 \\ \vdots \\ \\ y_{N} \end{array}\right]
\end{equation*}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgc6e14f88d5b166ecf7c29baaeb5d20e6.png)
Lower-triangular systems can be solved easily via forward substitution. It turns out that for this particular lower-triangular system, the solution can be computed easily by subtracting and dividing numbers in a table. To see how that works, please refer to Newton Divided Difference Application (wikipedia).
Further reading:
- Newton Polynomial (wikipedia).
