Math 753/853 HW2

Here is the Julia Notebook for HW2. Please download the notebook, fill it in, save your completed work as a notebook file with name math753-hw2-lastname.ipynb, and submit it either through Canvas or via email.

For your convenience reading online, the questions for HW2 are listed below.

Problem 1. Write a Julia function bisectsearch that take a function 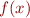$f(x)$ and an interval 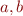$a,b$ such that 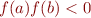$f(a) f(b) < 0$ , returns a root $r$ of $f$ within that interval. Find the root to as many digits accuracy as possible.

Challenges: (you don't have to do these, but you should do some if you want an A)

Add checks to your bisectsearch function that verify that the starting conditions for bisection search are met. The checks should print a helpful error message and exit the function while returning the most reasonable value for the root from available information.

Think carefully about the stopping conditions for bisection search. What kinds of problems are possible for this algorithm when it's implemented in floating-point arthmetic? Add checks to your function that stop iteration and return the most reasonable value for the root. In some cases you might want to print an error or warning message.

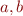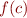Add some diagnostic printing to your function that prints out $a,b$ , and $f(c)$ at each iteration. Add another argument diagnostics to the function that turns the printing on and off. Make diagnostics default to false.

Write your bisectsearch function so that it operates equally well on any floating-point type: Float16, Float32, Float64, or BigFloat.

Instead of using if a; b; end statements for your checks, use the more Juliaesque a && b short-circuit conditional evaluation. Likewise, instead of using if a; b ; else c ; end statements, use the a ? b : c ternary operator. See http://docs.julialang.org/en/release-0.4/manual/control-flow/#man-conditional-evaluation.

Problem 2. Apply the bisection search algorithm to find all real roots of

(a) 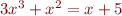$3x^3 + x^2 = x + 5$

(b) $\cos^2 x + 6 = x$

(c) $\ln x + x^2 = 3$

Problem 3. Write a Julia function newtonsearch that take a function 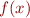$f(x)$ and an initial guess $x_0$ , and returns a root $r$ of $f$ using the Newton method. Find the root to as many digits accuracy as possible.

Challenges:

The Newton method requires the derivative 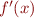$f'(x)$ as well as the function 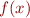$f(x)$ . How are you going to compute the derivative?

Unlike bisection, which is guaranteed to converge, the Newton method can go haywire. Think of a good way to test if the Newton method is failing, and print an error message and exit in this case. Your function should still return a number of the same floating-point type as $x_0$ . In Julia, this is known as type stability.

As in the bisection search challenges

think carefully about the appropriate stopping conditions for the search, given the finite precision of computer arithmetic
make sure your code operates equally well on all floating-point types.
add diagnostic printing to your code and turn it on/off with a diagnostics argument that defaults to false
use short-circuit boolean and ternary operators instead of if-then, where appropriate, to make your code more compact and readable

Problem 4. Apply the Newton method to find all real roots of

(a) 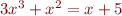$3x^3 + x^2 = x + 5$

(b) $\cos^2 x + 6 = x$

(c) $\ln x + x^2 = 3$

Problem 5. Modify your bisection-search and Newton-method functions so that, along with the root $r$ they return a vector of errors $e_n = | x_n - r|$ for $n=1,2,...$ . Then solve $\cos^2 x + 6 = x$ using both bisection and Newton method, and make a plot comparing $e_n$ versus $n$ for the two methods. Put both the bisection errors and the Newton method errors on the same plot. Use blue circles for bisection errors and red squares for Newton method. Make the vertical $e_n$ axis logarithmic.

We have theoretical estimates of the convergence rates of bisection and Newton method. Do your error plots fit this theory, or not? Explain your answer in reference to the error plots.

Bonus problem 6. Use your Newton-method function to find the root of 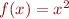$f(x) = x^2$ starting with initial guess $x_0=1$ , and plot the error $e_n$ versus $n$ as in problem. Does the Newton method converegence toward the true solution at the expected rate? Why or why not?

Bonus problem 7. Consider $f(x) = (1-3/(4x))^{1/3}$ . What is the root $r$ of this function? What happens when you apply your Newton-method algorithm to this function with a starting guess $x_0 = 1$ ? Why?

channelflow.org

User Tools

Site Tools

Math 753/853 HW2

Page Tools