The final exam takes place Wed 12/16 8:00am-10:0am in Horton 4. You must take the final exam at the scheduled time. No early exams or make-up exams will be offered.

The final exam is cumulative, including all topics covered in the course except power series. Think of the final exam as 2/3 (exam1 + exam2 + exam3 + systems of ODEs). There will be eight or so problems on the exam. You will have to decide which method to use for which problem.

You are allowed a cheat sheet of one 8 1/2 x 11 inch paper, both sides. You can put anything you want on the cheat sheet. You do not have to turn the cheat sheet in.

The outline of topics is as follows

• 1st order equations
  • separable
  • exact
  • 1st order linear
  • substitutions: Bernoulli, homogeneous*, and

• 2nd and higher-order equations
  • reduction of order
  • homogeneous constant coefficient ( is your friend)
  • judicious guessing
  • variation of parameters

• Laplace transforms
  • definitions, properties, and transforms & inverses of simple functions
  • s-translation, t-translation
  • Heaviside and Dirac delta functions

• Systems of linear equations
  • matrices, vectors, problems, and determinants
  • the eigenvalue problem, how it arises from the ODE 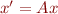and ansatz
  • how to solve systems of ODEs with
    • real eigenvalues, distinct
    • real eigenvalues, repeated
    • complex eigenvalues (solutions expressed in both complex and real-valued forms)
  • phase portraits

Several of the teaching assistants have final exams for their graduate course Wednesday afternoon and Thursday. We do not expect to start grading the final exam until Friday morning.