Math 445 lecture 10: more ''for''
The following example problem spells out in great detail how to translate a formula in summation notation into a Matlab for loop.
Recall this classic formula for 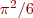 due to Euler:
due to Euler:

We can sum the first N terms of this series with the Matlab one-liner
N=100; sum((1:N).^(-2))
We can also do the sum with a for loop. To see how to build the for loop, it's helpful to think of the series as a sequence of partial sums

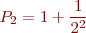
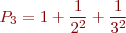
etc. Note that the difference between successive partial sums is a single term.

So we can compute the  th partial sum
th partial sum  by successively adding the term
by successively adding the term  for n going from 1 to N.
for n going from 1 to N.
That's exactly we do when we compute the sum with a for loop.
N=100; P=0; for n=1:N P = P + 1/n^2; end
At each step in the for loop, we compute  for the current value of
for the current value of  , add it to the previously computed partial sum
, add it to the previously computed partial sum  , and then store the result into
, and then store the result into  . But, since we are only interested in the final value
. But, since we are only interested in the final value  , we just store the current value of the partial sum in the variable P and write over it with the next value each time we step through the loop.
, we just store the current value of the partial sum in the variable P and write over it with the next value each time we step through the loop.
