IAM 961 HW2

Use Matlab to demonstrate how uniqueness works for complex matrices, along the lines of the SVD demo in lecture. Specifically

Case 1: Distinct singular values

Create a random 4 x 4 complex matrix 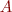$A$ with distinct singular values and known SVD $U_1 \Sigma_1 V_1^*$
Compute the SVD $U_2 \Sigma_2 V_2^*$ of $A$ .
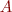Of the two SVDs, what should be the same? What is likely to be different?
Show that the third column of $V_1$ is “colinear” with the third column of $V_2$ , where the constant of linearity is a complex number with unit magnitude.
Do the same for the third columns of $U_1$ and $U_2$ . What is the relation between this constant and the constant of the previous question?

Case 2: Repeated singular values

Create a random 4 x 4 complex matrix 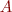$A$ with $\sigma_1 = \sigma_2 > \sigma_3 > \sigma_4$ and known SVD $U_1 \Sigma_1 V_1^*$
Compute the SVD $U_2 \Sigma_2 V_2^*$ of $A$ .
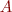Of the two SVDs, what should be the same? What is likely to be different?
Show that the first two columns of $U_1$ span the same 2d subspace as the first two columns of $U_2$ (do this by showing that the first two columns of $U_1$ are in the span of the first two columns of $U_2$ , and vice versa).

Keep a diary of your work in Matlab (diary on). Edit the diary text file to remove mistakes and extraneous material, and turn in a printout of the text file. Use comments to explain what you are doing, in the style of the SVD demo

channelflow.org

User Tools

Site Tools

IAM 961 HW2

Page Tools