Table of Contents
Math 445 lab 2: vectors, plots, and scripts
Do the problems for parts 1 and 2 at the Matlab prompt, saving your work to a file with the diary command.
Be kind to your teaching assistant!
- Label each problem with a Matlab comment (e.g. % ==== Problem 1 ====).
- For questions with free-form response, write your answer as a Matlab comment. Write in complete sentences!
- Reduce unnecessary whitespace with the
format compactcommand. - When you're done, edit the diary file to eliminate errors, so that your diary shows just the correct work.
- Add and subtract blank lines as necessary to make your work organized and easiy readable.
Part 1: Vector manipulation
Relevant Matlab
[] % square brackets , % row separator ; % col separator : % colon operator ' % apostrophe linspace
1. Assign a row vector with elements 3, 4, 5, 9 to the variable u.
2. Assign the transpose of u to the variable w.
3. Change the third element of w to 10.
4. Assign a column vector with the elements 7, 1, -2, 3 to the variable z.
5. Add w and z. Does the result make sense?
6. Add u and z. Does the result make sense?
7. Create a vector of the even integers between 2 and 14, inclusive.
8. Create a vector of the odd integers between 7 and 19, inclusive.
9. Make x a vector from 0 to  in increments of 0.02.
in increments of 0.02.
Part 2: Computing sums
Relevant Matlab syntax
: % colon operator sum % sum function .* ./ .^ % dot syntax
10. What is the sum of every third number between 3 and 27, inclusive?
11. What is the sum of the integers between 1 and 100, inclusive?
12. The infinite series
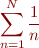
diverges as  . Demonstrate this in Matlab by computing the sum for several values of
. Demonstrate this in Matlab by computing the sum for several values of  , e.g.
, e.g.  to
to 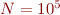 by powers of ten.
by powers of ten.
13. The  function can be calculated from the infinite series
function can be calculated from the infinite series
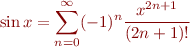
Of course we have to truncate this infinite sum to a finite number of terms in order to calculate it on a computer. How many terms do you need to keep in order to compute 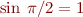 to sixteen digits accuracy?
Hint: use
to sixteen digits accuracy?
Hint: use format long to see all sixteen digits of the computation.
Are you amazed or what?
14. Now use the same infinite series for  to calculate
to calculate  . How many terms do you need to keep in order get the correct answer to sixteen digits accuracy?
. How many terms do you need to keep in order get the correct answer to sixteen digits accuracy?
Are you perplexed or what? What is strange about this calculation? Can you explain what happened?
Part 3: Plots
Relevant Matlab
.* ./ .^ % dot syntax plot % plot function axis % set limits on plot or aspect ratio xlim % set x limits ylim % set y limits grid % turn grid on/off help % help function
15. Make a plot of the polynomial 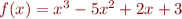 as a blue line. In the same plot, draw a line along the
as a blue line. In the same plot, draw a line along the  axis. (Hint: in Matlab create a zero vector of the same length as your
axis. (Hint: in Matlab create a zero vector of the same length as your  vector with
vector with y=0*x, then plot  versus
versus  along with
along with  versus
versus  .) Using this plot, estimate the zeros of the polynomial, i.e. the values of
.) Using this plot, estimate the zeros of the polynomial, i.e. the values of  for which
for which  . Make sure to find all the zeros of
. Make sure to find all the zeros of  by adjusting limits of the plot until all intersection of
by adjusting limits of the plot until all intersection of  with the
with the  -axis are visible.
-axis are visible.
16. Make a plot of a unit circle, i.e. a curve that satisfies 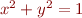 . Draw the circle with a thick red line, label the axes, and give the plot a title. Make sure the circle looks like a circle and not an oval. Hint: don't try to draw the plot using the equation
. Draw the circle with a thick red line, label the axes, and give the plot a title. Make sure the circle looks like a circle and not an oval. Hint: don't try to draw the plot using the equation 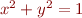 . Instead parameterize the curve in terms of the angle
. Instead parameterize the curve in terms of the angle  , i.e. calculate
, i.e. calculate  and
and  from
from  .
.
(I previously had a problem 17, revisiting the sum of  …to be written. But on second thought, this problem belongs in lab 3. So expect it there.)
…to be written. But on second thought, this problem belongs in lab 3. So expect it there.)