Math 445 Lab 6

Problem 1: Find all solutions of the equation 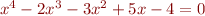$x^4 - 2x^3 -3x^2 + 5x - 4 =0$ in the following steps. Define a function 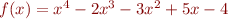$f(x) = x^4 - 2x^3 -3x^2 + 5x - 4$ using Matlab's anonymous function syntax. Define a vector x of gridpoints over some appropriate range using Matlab's linspace function. Plot 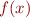$f(x)$ versus x and note the approximate values of x where $f(x) = 0$. Then find precise solutions by calling Matlab's fsolve function with the approximate solutions as initial guesses. Plug each precise solution back into 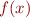$f(x)$ to show that fsolve in fact produces numerically accurate solutions.

Problem 2: Write an f2c(f) and a c2f(c) function that convert Farenheit temperatures to Celsius and vice versa. Each function should print a statement of the form 

For input 32 F, the output is 0 C

or 

For input 100 C, the output is 212 F

and then return the correct converted temperature. Write the functions in files f2c.m and c2f.m. Make sure the functions are correct by checking that the above equivalent temperatures are converted correctly, and by computing f2c(c2f(x)) and c2f(f2c(x)) for a variety of values of x.

Note: problems 3,4, and 5 use names like mymean to avoid conflicts with similar built-in Matlab functions.

Problem 3: Write a function mymean(x) that computes the mean value of the elements in the input vector x according to the formula

\begin{eqnarray*} \text{mean}(x) = \frac{1}{N} \sum_{i=1}^N x_i \end{eqnarray*}

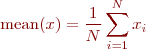
where N is the number of elements. Compute this sum with a for loop. Figure out a good way to test your function and test it.

Problem 4: Write a function mystd(x) that computes the standard deviation of the elements in the input vector x according to the formula

\begin{eqnarray*} \text{std}(x) = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \bar{x})^2} \end{eqnarray*}

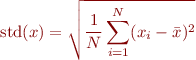
where N is the number of elements in the vector x and $\bar{x}$ is the mean of x. Figure out a good way to test your function and test it.

Problem 5: Write a function mygeomean(x) that computes the geometric mean of the elements in the input vector x according to the formula

\begin{eqnarray*} \text{geomean}(x) = \sqrt[N]{\prod_{i=1}^N |x_i|} \end{eqnarray*}

Figure out a good way to test your function and test it.