Math 445 lab 4: dot syntax and plotting

Problem 1: Create a plot that shows $\sin x$ and $\cos x$ over $-\pi \leq x \leq \pi$ with the sine in green and the cosine in blue. Choose enough gridpoints that the curve looks smooth. Label the $x$ axis and use a legend to label the curves.

Helpful Matlab commands: linspace, plot, xlabel, legend, help.

Problem 2: Consider the two functions $f(x) = x^n$ and $g(x) = n^x$ for the fixed value $n=5$ . Which function increases faster as $x \rightarrow \infty$ ? (Hint: plot the two functions together on the range $0 \leq x \leq 100$ , and plot the $y$ axis logarithmically.) Would the answer change if you increased the value of $n$ ?

Helpful Matlab commands: linspace, semilogy, xlabel, legend, help, plus dot-syntax.

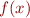Problem 3: How many real roots does the function $f(x) = x^3 - 5x^2 + 2x + 4$ have? Determine this by plotting the $f(x)$ and counting how many times it crosses zero. Estimate the roots graphically to two digits by refining your plots in the neighborhood of each zero crossing.

Helpful Matlab commands: linspace, plot, xlabel, ylabel, axis, plus dot-syntax. In particular you can use axis([xmin xmax ymin ymax]) to zoom in on regions near zeros. Or you can zoom in by refining the range of $x$ and replotting.

Problem 4: The exponential function $e^x$ can be computed from the power series

$\begin{eqnarray*} e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \end{eqnarray*}$

In practice one truncates the infinite sum to a finite number of terms, summing from $n=0$ to $n=N$ for some fairly large $N$ . How large does $N$ need to be to calculate $e^2$ to sixteen digits? You can answer this question very quickly by writing one line of Matlab code that evaluate the truncated sum for a fixed value of $N$ , and then rerunning it with changing values of $N$ .

Helpful Matlab commands: sum, format, exp (for getting the correct value of $e$ to sixteen digits), colon syntax, dot syntax, and log10 (for counting digits of precision).

Problem 5: The sine function can be computed from the power series

$\begin{eqnarray*} \sin x = \sum_{n=0}^\infty (-1)^n \frac{x^{2n+1}}{(2n+1)!} \end{eqnarray*}$

Like the exponential function, in practice one truncates this sum at $n=N$ . How large does $n$ need to be to calculate $\sin \pi/3$ to sixteen digits?

Helpful Matlab commands: same as problem 4.