Math 445 Lab #1
Most of these problems are taken from Attaway chapter 1, both 2nd and 3rd editions. Remember, Matlab's help function is your friend.
Problem 1: Evaluate these Matlab expressions in your head and write down the answer. Then type them into Matlab and see how Matlab evaluates them. If you made a mistake, figure out what it was.
25/4*4
3+4^2
4\12 + 4
3^2
(5-2)*3
Problem 2: Translate these mathematical expressions into Matlab expressions, and then evaluate them.
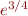
![Math $\sqrt[5]{7}$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img8eba0c2fac42939c8a6b377f48b1dd13.png)
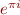
cube root of 19
3 to the 1.2
tangent of 
Problem 3: Wind chill factor: The WCF supposedly conveys how cold it feels with a given air temperature T (degrees Farenheit) and wind speed V (miles per hour). A formula for WCF is

Create variables for temperature T and wind speed V and then using this formula, calculate the WCF for (a) T = 45 F and V = 10 mph and (b) T = 45 F and V = 0 mph.
Problem 4: The geometric mean g of n numbers  is given by
is given by
![Equations \begin{eqnarray*}
g = \sqrt[n]{x_1 x_2 \ldots x_n}
\end{eqnarray*}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgc479d6fc85938a81b6a113e9f7a25ade.png)
This is useful, for example, in finding the average rate of return on an investment with varying yearly return.
(a) If an investment returns 15% its first year, 5% its second, and 10% its third, the average rate of return is
![Equations \begin{eqnarray*}
\sqrt[3]{1.15 \cdot 1.05 \cdot 1.10}
\end{eqnarray*}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgffdafd233af0d1ccbdc3ed655b7cb8c3.png)
Compute the average rate of return, expressed as a percent.
(b)Which is better, a steady 5% per year return on investment, or alternating between 0% and 10% year by year?
Problem 5: The astoundingly brilliant but short-lived mathematician Srinivasa Ramanujan devised the following very powerful formula for for 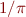
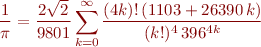
You can get an approximation of  using only arithmetic operations by evaluating and summing a finite number of terms of this series. What is the numerical approximation of
using only arithmetic operations by evaluating and summing a finite number of terms of this series. What is the numerical approximation of  using just the first term (
using just the first term ( )? Using the first and second (
)? Using the first and second ( and
and 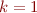 )? How many digits of accuracy does each of these approximation have? Be sure to use
)? How many digits of accuracy does each of these approximation have? Be sure to use format long.
(adapted from a problem in Introduction to Matlab Programming by Siauw and Bayen)
Problem 6: Translate the following Matlab logical expressions into English.
x < y x < y || y < z x <= y && y <= z
Problem 7: Translate the following mathematical expressions into Matlab and evaluate for 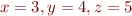 .
.
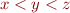
 and
and 
 or
or 
Problem 8: Evaluate the following Matlab expressions and explain the results.
3 == 4 ~(5 >= 2) 2 < 3 < 5 2 > 3 > 5 2 > 3 < 5 xor(5 < 6, 8 > 4) (3 == 2) + 1
Problem 9: If P is a logical expression, the law of noncontradiction states that P AND (NOT P) is always false. Use Matlab to verify this for both P false and P true.
Problem 10: Let P and Q be logical expressions. De Morgan's rule states that NOT (P OR Q) = (NOT P) AND (NOT Q) and also that NOT (P AND Q) = (NOT P) OR (NOT Q). Demonstrate with Matlab that both these rules hold for all possible combinations of P and Q.
Problem 11: Construct an equivalent logical expression for P OR Q using only AND and NOT. Translate that into Matlab and then test for all possible values of P and Q. Write your demonstration in the following fashion, in order to make it easy to follow
P=0; Q=0; (my expression) == (P || Q) P=1; Q=0; (my expression) == (P || Q)
etc.
Problem 12: Construct an equivalent logical expression for P AND Q using only OR and NOT. Translate that into Matlab and then test for all possible values of P and Q. Folow the same kind of pattern as in problem 11.