Math 445 HW5
This homework is meant as review for the second-chance exam to be held Nov 26. It is due Thursday Nov 14th in lecture.
Review topics
- fprintf: formatted printing function
- plotting:
plot, contour, surf, mesh, meshgrid - loops:
forandwhile - anonymous functions: defining and using
- solving equations: with
fsolveornewtonsearch - monte carlo simulation
- log-linear relationships:
semilogy, semilogx, loglog - index operations
Problem 1: Find all real-valued solutions of the equation  by plotting
by plotting 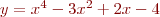 versus
versus  , estimating the values of
, estimating the values of  where
where
 , and then solving the equation numerically using those estimates as initial
guesses. Turn in your plot, your matlab code, and the numerical solutions to the equation.
, and then solving the equation numerically using those estimates as initial
guesses. Turn in your plot, your matlab code, and the numerical solutions to the equation.
Problem 2: Define a rightshift function using Matlab's anonymous function facility
that shifts the elements of a row vector one step to the right, wrapping the last element
around to the first position. For example rightshift([1 2 3 4]) should return [4 1 2 3].
Problem 3: Write Matlab code to estimate the probability of drawing four-of-a-kind from a randomly shuffled 52 card deck. Turn in your code and your estimated probability.
Problem 4: Make a 3d plot of  versus
versus  for the function
for the function 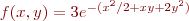 for
for  and
and  , on a mesh with
, on a mesh with  . Use Matlab's
. Use Matlab's meshgrid function.
Problem 5: Print  to five digits accuracy. (Hint: You get
to five digits accuracy. (Hint: You get  in Matlab from
in Matlab from exp(1)).
Problem 6: Write an isPrime(n) function that returns 1 (true) if n is prime and
0 (false) for a composite. Don't worry about efficiency, just loop over 2 and the odd integers
less than or equal to  , and return 0 if any divide
, and return 0 if any divide n evenly, and 1 if not.
(You might have already done this as an optional problem for exam 1 prep.)
Problem 7: Write Matlab code that will compute the first 20 prime numbers, using your
isPrime function from problem 6.
Problem 8: Deduce the functional relationship between  and
and  for the data shown in this plot
for the data shown in this plot
Bonus: Write an primes(N) function that returns all primes less than or equal to N
using the Sieve of Eratosthenes algorithm.
