Selected problems from Attaway 3rd edition, chapters 1 and 2.

Problem 1: Create the following vectors twice, once using linspace and once using the colon operator. 

1 2 3 4 5 6 7 8 9 10

2 7 12

Problem 2: Use the colon and transpose operators to create a column vector that has values -1 to 1 in steps of 0.2.

Problem 3: Given a vector v of arbitrary length, write an expression that evaluates to the odd-numbered elements of v. Test your expression on vectors v of both even and odd length.

Problem 4: Given a vector v of arbitrary length, write assignment statements that store the first half of v in a vector v1 and the second half in a vector v2. Make sure your assignment statements work for v of both even and odd length.

Problem 5: Create a 4 x 2 matrix of all zeros and store it in a variable. Then replace the second row of the matrix with a 3 and a 6.

Problem 6: Create a 3 x 5 matrix of random real numbers, and then delete the third row.

Problem 7: What are the values of the following expressions? Explain why. 

'c' == 'd' - 1 && 2 < 4
'c' == 'd' - 1 || 2 < 4
xor('c' == 'd' - 1, 2 < 4)
10 > 5 > 2

Problem 8: The value of 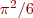$\pi^2/6$ can be approximated by the sum of the series

1 + 1/2^2 + 1/3^2 + 1/4^2 + \ldots

Write a one-line Matlab expression that evaluates the sum for the first $n$ terms. Test it for a few values of $n$ and compare to $\pi^2/6$.

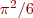Problem 9: A vector v stores hours worked and hourly wages sequentially for a number of employees. For example 

  v = [33 10.5 40 18 20 7.5]

would specify three employees, the first working for 33 hours at $10.50/hr, the second 40 hours at $18/hr, etc. For an arbitrarily long v, write code that would separate v into an h vector of hours worked and a r vector of hourly wage rates, and then compute a w vector of wages owed to each employee. Do this as compactly as possible.

Problem 10: Evaluations at a university are scored 1-5, bad to good. However the evaluation forms mistakenly say that 1-5 is good to bad. So the computer program written to analyze evaluations must “reverse” all the evaluation scores. That is, 

evals = [5 3 2 5 5 4 1 2]

should really be 

evals = [1 3 4 1 1 2 5 4]

Write Matlab code that will reverse an arbitrary eval vector to the correct 1-5 scale.